Symmetry Planes
Geometric symmetry, electric symmetry and magnetic planes of symmetry in a model can be exploited to reduce runtime and memory requirements.
Symmetry in a model applies to the method of moments (MoM) and all hybrid techniques where the MoM is involved, but not in conjunction with the multilevel fast multipole method (MLFMM).
A symmetric model without geometric symmetry defined is not guaranteed to have a symmetric mesh. Such a setup leads to non-symmetric current distributions on the structure.
Geometric Symmetry
The structure must be symmetric concerning the symmetry plane, while the sources may be arbitrarily located.
Electric Symmetry
- The model must be geometric symmetry at the plane.
- The electric current density must be anti-symmetric.
- The magnetic current density must be symmetric.
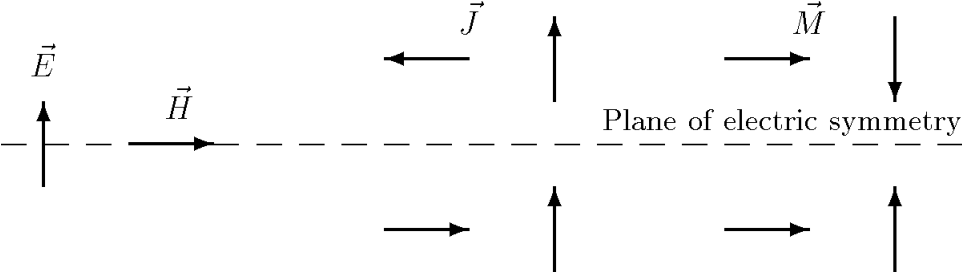
Figure 1. Electric symmetry plane
Magnetic Symmetry
- The model must be geometric symmetry at the plane.
- The electric current density must be symmetric.
- The magnetic current density must be anti-symmetric.
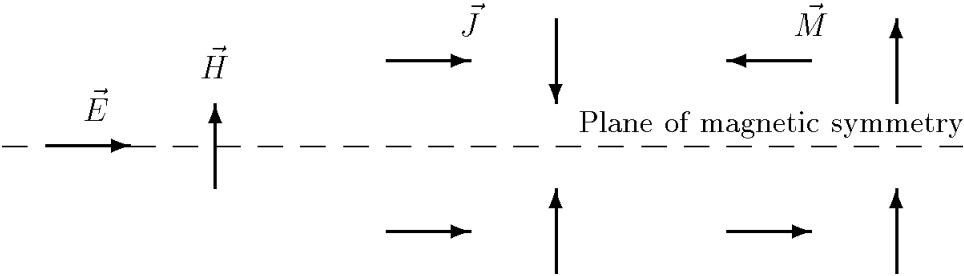
Figure 2. Magnetic symmetry plane