How Masks are Used for Optimisation
Perform complex optimisations with masks by specifying a variable goal. Apply the mask correctly to avoid undesired results.
See Figure 1 for a graphical representation of the mask. This is useful for validating that the mask data is correct, particularly when working with a large number of data points imported from an external file.
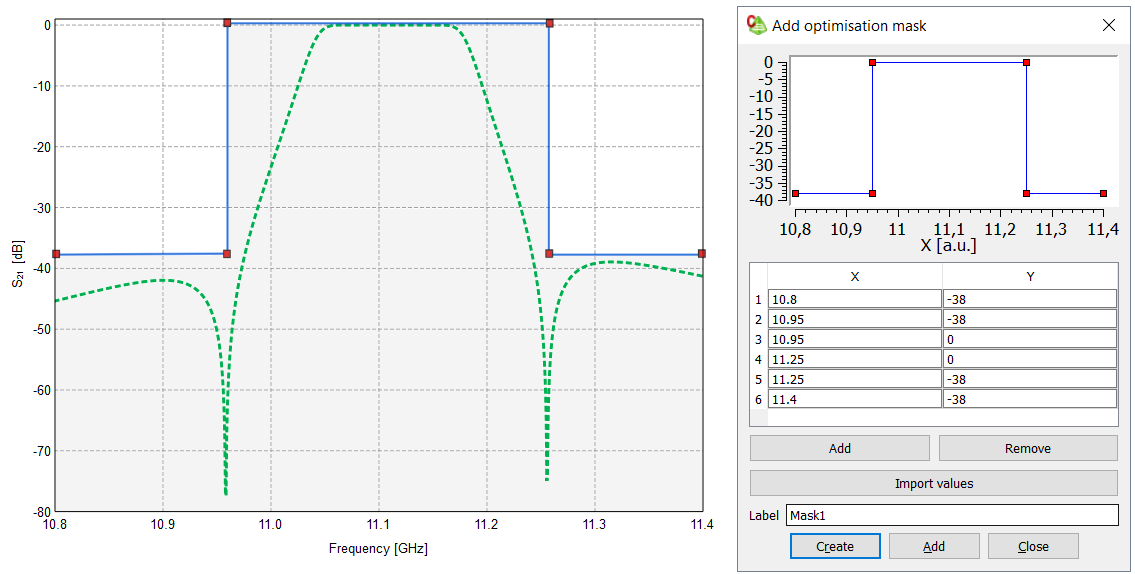
Figure 1. The desired frequency response of a Ku-band waveguide filter (indicated in green) with a mask (indicated in blue) and (b) the Add optimisation mask dialog.
All the calculated points that satisfy the criteria for the goal type and name are added to a long array of values and then compared to the mask. The following examples illustrate the usage of masks during optimisation.
Example 1: Optimisation of a Far Field Pattern at a Single Frequency
Create the mask with the required shape and the far field request that is compared to the mask. The first point (angle) in the far field calculation map to the first point in the mask and the last point (angle) in the far field calculation map to the last point in the mask. All other points of the far field is compared to points in the mask (linear interpolation is used to ensure a continuous mask).
Example 2: Optimisation for a Specific Gain Profile over Frequency
Create the far field request containing a single far field point. There after create the mask that contains the gain profile over frequency. The gain at the first frequency map to the first point in the mask and the gain at the last frequency map to the last point in the mask. The gain at the frequency values within the range are compared to the values in the mask using linear interpolation.
Example 3: Optimisation for a Varying Far Field (Gain) Profile Over Frequency
Using a combination of the two examples above create a complex optimisation requiring a predefined far field/gain pattern that changes as a function of frequency. Create the multi-point far field requests for each frequency. There after create a mask that the first point of the mask map to the first point in the far field request at the first frequency. The last point in the mask map to the last point of the far field request of the last frequency. If the required far field pattern is unchanged over frequency then the mask contains the same far field pattern repeated N times, where N is the number of frequency points.