Source Methods and Field Methods
Solver methods can be categorized as either source-based methods or field-based methods. Understanding the main differences between these two categories helps to understand and choose an appropriate solution method for each application.
Discretization
In source methods, only the structure is discretized (meshed) but not the free-space regions between the structures. In field methods, the whole solution domain is discretized, that is the structure as well as the free-space region between structures.
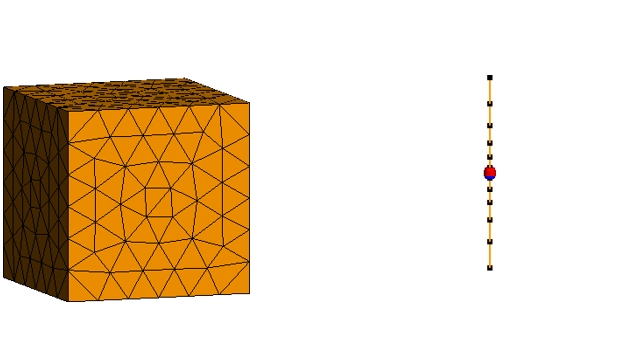
Figure 1. A dipole and cuboid discretized for a source-based solution.

Figure 2. A dipole and cuboid discretized for a field-based solution.
Boundary Conditions
In field-based methods, the propagating fields, and therefore the fields' associated mesh, requires a proper termination (truncation). This is not a problem for closed regions such as waveguides or cavities where the PEC boundary provides a proper termination. However, for open radiating problems such as shown in Figure 1 and Figure 2, the mesh would be required to extend to infinity. An artificial absorbing region within the mesh is used to solve this problem. This termination or absorbing region is denoted a boundary condition. Source-based methods do not require a termination of the mesh (boundary condition). A special function (denoted the Green's function) built into the method automatically accounts for the field behaviour at infinity or any point in space.1
Solvable Model Size
Field-based methods are generally more limited in terms of the size, specifically the electrical size (in wavelengths), of models they can solve. This is because a growing model size implies a larger volume of mesh elements to mesh and solve. For source-based methods it is only a larger surface area of mesh elements. It is assumed, however, that acceleration techniques for the source-based method is employed such as the multilevel fast multipole method. In addition it must be noted that increasing usage of GPU acceleration is increasing the solvable sizes of field-based models.