Nonlinear Behavior
The force and moment in a spring is computed as:
(1)
F
i
(
δ
i
)
=
f
(
δ
i
A
s
c
a
l
e
i
)
[
A
i
+
B
i
ln
(
max
(
1
,
|
δ
˙
i
D
i
|
)
)
+
E
i
g
(
δ
˙
i
F
i
)
]
+
C
i
δ
˙
i
+
H
s
c
a
l
e
i
h
(
δ
˙
i
F
i
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakqaabeqaaiGacA
eadaWgaaWcbaGaamyAaaqabaGcdaqadaqaaiabes7aKnaaCaaaleqa
baGaamyAaaaaaOGaayjkaiaawMcaaiabg2da9iGacAgadaqadaqaam
aalaaabaGaeqiTdq2aaWbaaSqabeaacaWGPbaaaaGcbaGaamyqaiaa
dohacaWGJbGaamyyaiaadYgacaWGLbWaaSbaaSqaaiaadMgaaeqaaa
aaaOGaayjkaiaawMcaamaadmaabaGaamyqamaaBaaaleaacaWGPbaa
beaakiabgUcaRiaadkeadaWgaaWcbaGaamyAaaqabaGcciGGSbGaai
OBamaabmaabaGaciyBaiaacggacaGG4bWaaeWaaeaacaaIXaGaaiil
amaaemaabaWaaSaaaeaacuaH0oazgaGaamaaCaaaleqabaGaamyAaa
aaaOqaaiaadseadaWgaaWcbaGaamyAaaqabaaaaaGccaGLhWUaayjc
SdaacaGLOaGaayzkaaaacaGLOaGaayzkaaGaey4kaSIaamyramaaBa
aaleaacaWGPbaabeaakiGacEgadaqadaqaamaalaaabaGafqiTdqMb
aiaadaahaaWcbeqaaiaadMgaaaaakeaacaWGgbWaaSbaaSqaaiaadM
gaaeqaaaaaaOGaayjkaiaawMcaaaGaay5waiaaw2faaaqaaiaaywW7
cqGHRaWkcaaMe8Uaam4qamaaBaaaleaacaWGPbaabeaakiqbes7aKz
aacaWaaWbaaSqabeaacaWGPbaaaOGaey4kaSIaamisaiaadohacaWG
JbGaamyyaiaadYgacaWGLbWaaSbaaSqaaiaadMgaaeqaaOGaciiAam
aabmaabaWaaSaaaeaacuaH0oazgaGaamaaCaaaleqabaGaamyAaaaa
aOqaaiaadAeadaWgaaWcbaGaamyAaaqabaaaaaGccaGLOaGaayzkaa
aaaaa@82E9@
Where,
i
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGPbaaaa@374C@
is the translational degrees of freedom: 1,2,3
(2)
M
i
(
θ
i
)
=
f
(
θ
i
A
s
c
a
l
e
i
)
[
A
i
+
B
i
ln
(
max
(
1
,
|
θ
˙
i
D
i
|
)
)
+
E
i
g
(
θ
˙
i
F
i
)
]
+
C
i
θ
˙
i
+
H
s
c
a
l
e
i
h
(
θ
˙
i
F
i
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakqaabeqaaiGac2
eadaWgaaWcbaGaamyAaaqabaGcdaqadaqaaiabeI7aXnaaCaaaleqa
baGaamyAaaaaaOGaayjkaiaawMcaaiabg2da9iGacAgadaqadaqaam
aalaaabaGaeqiUde3aaWbaaSqabeaacaWGPbaaaaGcbaGaamyqaiaa
dohacaWGJbGaamyyaiaadYgacaWGLbWaaSbaaSqaaiaadMgaaeqaaa
aaaOGaayjkaiaawMcaamaadmaabaGaamyqamaaBaaaleaacaWGPbaa
beaakiabgUcaRiaadkeadaWgaaWcbaGaamyAaaqabaGcciGGSbGaai
OBamaabmaabaGaciyBaiaacggacaGG4bWaaeWaaeaacaaIXaGaaiil
amaaemaabaWaaSaaaeaacuaH4oqCgaGaamaaCaaaleqabaGaamyAaa
aaaOqaaiaadseadaWgaaWcbaGaamyAaaqabaaaaaGccaGLhWUaayjc
SdaacaGLOaGaayzkaaaacaGLOaGaayzkaaGaey4kaSIaamyramaaBa
aaleaacaWGPbaabeaakiGacEgadaqadaqaamaalaaabaGafqiUdeNb
aiaadaahaaWcbeqaaiaadMgaaaaakeaacaWGgbWaaSbaaSqaaiaadM
gaaeqaaaaaaOGaayjkaiaawMcaaaGaay5waiaaw2faaaqaaiaaywW7
cqGHRaWkcaaMb8UaaGjbVlaadoeadaWgaaWcbaGaamyAaaqabaGccu
aH4oqCgaGaamaaCaaaleqabaGaamyAaaaakiabgUcaRiaadIeacaWG
ZbGaam4yaiaadggacaWGSbGaamyzamaaBaaaleaacaWGPbaabeaaki
GacIgadaqadaqaamaalaaabaGafqiUdeNbaiaadaahaaWcbeqaaiaa
dMgaaaaakeaacaWGgbWaaSbaaSqaaiaadMgaaeqaaaaaaOGaayjkai
aawMcaaaaaaa@84E0@
Where,
i
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGPbaaaa@374C@
is the rotational degrees of freedom: 4,5,6
The variables in the force and moment equation represent:
f
(
δ
i
A
s
c
a
l
e
i
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGMbWaae
WaaeaadaWcaaqaaiabes7aKnaaCaaaleqabaGaamyAaaaaaOqaaiaa
dgeacaWGZbGaam4yaiaadggacaWGSbGaamyzamaaBaaaleaacaWGPb
aabeaaaaaakiaawIcacaGLPaaaaaa@4238@
Spring force versus displacement function input as
fct_ID 1i
f
(
θ
i
A
s
c
a
l
e
i
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGMbWaae
WaaeaadaWcaaqaaiabeI7aXnaaCaaaleqabaGaamyAaaaaaOqaaiaa
dgeacaWGZbGaam4yaiaadggacaWGSbGaamyzamaaBaaaleaacaWGPb
aabeaaaaaakiaawIcacaGLPaaaaaa@4249@
Spring force versus rotation function input as
fct_ID 1i
A
i
,
B
i
,
D
i
,
E
i
and
F
i
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9
pgeaYRXxe9vr0=vr0=vqpWqaaiaaciWacmaadaGabiaaeaGaauaaaO
qaaiaadgeadaWgaaWcbaGaamyAaaqabaGccaqGSaGaaeiiaiaadkea
daWgaaWcbaGaamyAaaqabaGccaqGSaGaaeiiaiaadseadaWgaaWcba
GaamyAaaqabaGccaqGSaGaaeiiaiaadweadaWgaaWcbaGaamyAaaqa
baGccaqGGaGaaeyyaiaab6gacaqGKbGaaeiiaiaadAeadaWgaaWcba
GaamyAaaqabaaaaa@4ACC@
Scaling coefficients
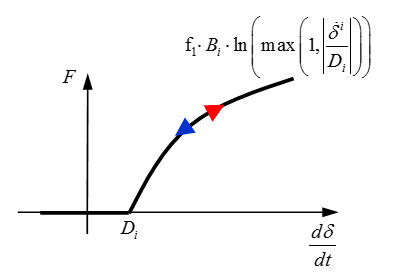
ln
(
max
(
1
,
|
δ
˙
i
D
i
|
)
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGSbGaai
OBamaabmaabaGaciyBaiaacggacaGG4bWaaeWaaeaacaaIXaGaaiil
amaaemaabaWaaSaaaeaacuaH0oazgaGaamaaCaaaleqabaGaamyAaa
aaaOqaaiaadseadaWgaaWcbaGaamyAaaqabaaaaaGccaGLhWUaayjc
SdaacaGLOaGaayzkaaaacaGLOaGaayzkaaaaaa@4785@
Logarithmic function that scales the spring
stiffness as the velocity increases
Figure 1. With Parameter Input
g
(
δ
˙
i
F
i
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGNbWaae
WaaeaadaWcaaqaaiqbes7aKzaacaWaaWbaaSqabeaacaWGPbaaaaGc
baGaamOramaaBaaaleaacaWGPbaabeaaaaaakiaawIcacaGLPaaaaa a@3DA6@
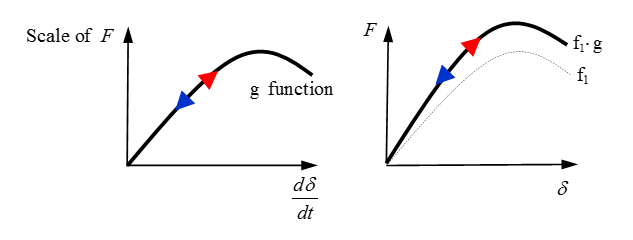
Scale the stiffness as a function of linear input as
fct_ID 2i
g
(
θ
˙
i
F
i
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGNbWaae
WaaeaadaWcaaqaaiqbeI7aXzaacaWaaWbaaSqabeaacaWGPbaaaaGc
baGaamOramaaBaaaleaacaWGPbaabeaaaaaakiaawIcacaGLPaaaaa a@3DB7@
Scale the moment as a function of rotational
velocity input as fct_ID 2i
This input can be used to model nonlinear strain rate effects of the spring
stiffness.
Figure 2. With g Function Input
C
i
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGdbWaaS
baaSqaaiaadMgaaeqaaaaa@3840@
Linear damping coefficient used to increase the
spring stiffness as a function of velocity
h
(
δ
˙
i
F
i
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGObWaae
WaaeaadaWcaaqaaiqbes7aKzaacaWaaWbaaSqabeaacaWGPbaaaaGc
baGaamOramaaBaaaleaacaWGPbaabeaaaaaakiaawIcacaGLPaaaaa a@3DA7@
or
h
(
θ
˙
i
F
i
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGObWaae
WaaeaadaWcaaqaaiqbeI7aXzaacaWaaWbaaSqabeaacaWGPbaaaaGc
baGaamOramaaBaaaleaacaWGPbaabeaaaaaakiaawIcacaGLPaaaaa a@3DB8@
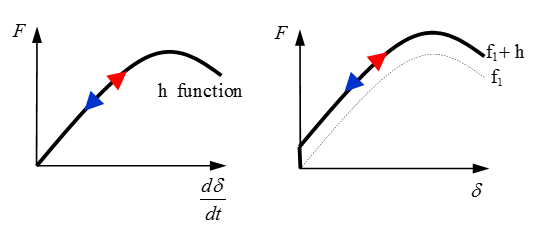
Nonlinear damping function input as
fct_ID 4i
Linear or nonlinear damping as a function of velocity can also be added to the spring
force using either a linear damping coefficient or a user-defined function.
Figure 3. With
h
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGNbaaaa@374B@
Function Input
The functions
g
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGNbaaaa@374B@
and
h
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGNbaaaa@374B@
both describe the damping behavior of the spring.
However, the
g
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGNbaaaa@374B@
function scales the spring stiffness function
f
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGNbaaaa@374B@
, but the
h
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGNbaaaa@374B@
function adds to the spring stiffness function
f
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGNbaaaa@374B@
.