|
»Click here to display Table of Contents«
|
sphere partial subpanel (Surfaces panel) |
|
|
|
|
|
sphere partial subpanel (Surfaces panel) |
|
|
|
|
This subpanel creates three-dimensional partial sphere surface primitives.
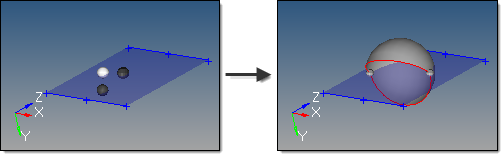
Eight inputs are required to create a sphere using this method:
| • | The center node defines the center of the sphere. |
| • | The vector between the center node and R node node defines the first axis of the sphere. |
| • | Either a phi node or a theta node to define the second axis and complete the definition of the sphere's orientation. |
If the theta node is specified, the theta zero degree angle starts on the vector between the center and R node nodes, and rotates in the plane created by the center, R node, and theta nodes. This plane also therefore defines the axis for phi, which starts its zero degree angle on the vector extending from the center node normal to the plane defined by the center, R node, and theta nodes.
If the phi node is specified, the phi zero degree angle starts on the vector between the center and R node nodes, and rotates in the plane created by the center, R node, and phi nodes. This plane also therefore defines the axis for theta, which starts its zero degree angle on the vector extending from the center node normal to the plane defined by the center, R node, and phi nodes.
| • | The radius defines the sphere radius. |
| • | The theta begin defines the starting angle for theta. Valid values for theta are from 0.0 to 360.0. |
| • | The theta end defines the ending angle for theta. |
| • | The phi begin defines the starting angle for phi. Valid values for phi are from 0.0 to 90.0. |
| • | The phi end defines the ending angle for phi. |
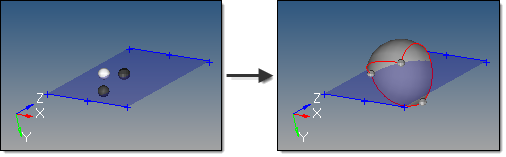
This example uses theta begin 45, theta end 270, phi begin -30, and phi end 90, while the previous
example uses the same theta values but phi values from -90 to 90.
Create partial sphere surface primitives
