Frequency domain filter implementation

The dual nature of time and frequency domains means a filter in the time domain can be equivalently implemented in the frequency domain. Depending on the application, however, one domain is usually more convenient to work in than the other.

A recursive IIR filter can be implemented in the frequency domain by taking the product of the frequency domain equivalents of the input sequence and the filter.

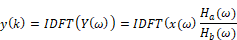
Here, X(ω) and Y(ω) are the Discrete Fourier Transforms (DFT) of the input and the output sequences respectively, and IDFT represents the Inverse Discrete Fourier Transform operation. H_a(ω) and H_b(ω) are the DFTs of the filter coefficients a_i and b_j, respectively, as given by the following difference equation:

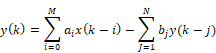
The DFT’s H_a(ω) and H_b(ω) must be of the same length as X(ω) and Y(ω). To accomplish this, the filter coefficients must be zero-padded appropriately. Consequently, the frequency domain implementation is computationally inefficient and will not be discussed further.