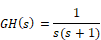
Consider a type 1 system with the open-loop transfer function:
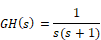
as shown below:
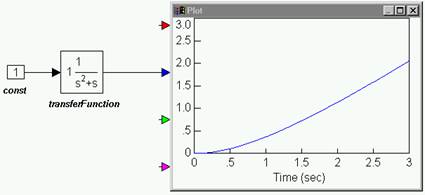
To generate the Nyquist plot
1. Create the above diagram using a const, transferFunction, and plot block.
2. Enter the following polynomial coefficients to the transferFunction block:
Numerator: 1
Denominator: 1 1 0
Note: Always leave spaces between coefficient values.
3.
Choose System > Go, or click 
in the toolbar to simulate the diagram.
4. Select the transferFunction block.
5. Choose Analyze > Nyquist Response.
6. You are reminded that the system has poles on the imaginary axis, which will result in Nyquist circles at infinity. Click OK, or press ENTER.
7. In the Nyquist dialog box, you have the option to change the maximum frequency range. The default value is 10. Leave it unchanged and click OK, or press ENTER.
8. The Nyquist plot appears.
9. Drag on its borders to adjust its size.
You can observe that the point (-1,0) is not enclosed by the Nyquist contour. Consequently N ≤ 0. The poles of GH(s) at s = 0 and s = -1, neither of which are in the right-half plane, which means that P = 0. Therefore, N = -P = 0 and the system is absolutely stable.