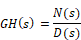
A root locus plot computes the locus of closed-loop poles for a transfer function while it’s under gain feedback. The gain is swept over a wide range of values, typically from a small value near zero to a larger one.
For brevity, the transfer function can be denoted as GH(s), which represents a ratio of polynomials in s, and can be written as:
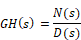
where N(s) is the numerator polynomial and D(s) is the denominator polynomial. The root locus gain is represented as K.
The following diagram presents the structure Embed uses to perform the Root Locus command calculations:
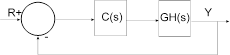
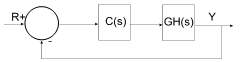
The closed-loop poles are the roots of the characteristic equation (or denominator of the closed-loop transfer function) and can be computed as the roots of:
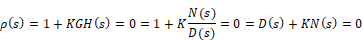
For small values of K, the closed-loop poles are approximately the roots of D(s) = 0 (the open-loop poles); and for large values of K (positive or negative), the closed-loop poles are approximately the roots of N(s) = 0 (the open-loop zeros). The root locus plot presents the paths of the closed-loop poles as the value of K varies.