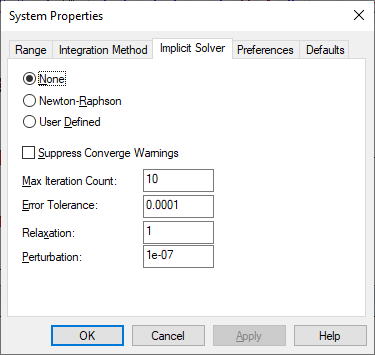
When solving an implicit equation, you can use the Newton Raphson solver or a custom solver. You can also set the error tolerance, maximum iteration count, perturbation, and relaxation parameters. After you choose the options you want, you can start the simulation.
To solve an implicit equation
1. Choose System > System Properties and click the Implicit Solver tab.
2. Choose the options you want, then click OK, or press ENTER.

Error Tolerance: Specifies the maximum allowable difference in total error between two successive iterations. A total error is computed as the sum of individual errors squared, where the error signal is the input signal to a constraint block. Newton-Raphson ceases iterating when the difference in total error between two successive iterations becomes less than the tolerance.
Use Error Tolerance in conjunction with Max Iteration Count to control the time spent converging. The larger the tolerance, the quicker and less accurate the solution. The default value is 0.0001.
Max Iteration Count: Specifies the number of iterations the solver performs while attempting to meet the error tolerance criterion. One iteration of the solver has many simulation runs to obtain the local n-dimensional surface and run downhill one step.The default value is 10.
None: When you’re not solving an implicit equation, activate None.
Newton-Raphson: Newton-Raphson is a singular value decomposition-based solver (SVD) that performs static optimization at each time step. Embed derives an n-dimensional slope by numerically perturbing the unknown outputs and observing the effects on the constraints. Embed uses the slope matrix to compute values for the unknown blocks that drive the constraints to a minimum.
Specifically, Newton-Raphson forms a Jacobian matrix of the partial derivatives of each unknown block on each constraint block by numerically adding a small offset (perturbing) for each unknown and seeing how it affects each constraint input. If an unknown block has no effect on a constraint block, the value at that element in the Jacobian is 0. The unknown block outputs are adjusted by the current error vector (vector of constraint inputs squared) divided by the Jacobian matrix. This is calculated using SVD. The unknown block updates are scaled by the Relaxation parameter. You should start with 1 and reduce if nonlinearities result in numerical instability. The perturbation value is the small offset used to calculate the Jacobian. It should be about 1% of the value of the smallest unknown. If it is too small (< max unknown*1e-13) then its effect can be lost and the unknown block will not factor into the Jacobian. The Error Tolerance is the sum of squares of all constraint inputs.
Newton-Raphson is particularly useful for solving static equations in the presence of concurrent dynamics.
Perturbation: Indicates the value by which the unknown blocks are numerically perturbed to evaluate the Jacobean (matrix of first partials). Each element of the Jacobean is a ratio of constraint change with respect to block perturbation value applied to the unknown blocks. The perturbation value should be at least one order of magnitude less than the unknown initial value, but greater than 1e-12 of the initial value for the unknowns. The default value is 1e-007.
Relaxation: Attenuates the iteration update value to attain convergence for equations that prove difficult to converge. As a side effect, it slows the convergence process because it forces the iteration to take smaller steps. The typical range is from slightly greater than 0 to 2. Select values less than 1 for systems that appear to be unstable. The default value is 1.
Suppress Convergence Warnings: If you’re solving for a set of roots that are equidistant from zero, you must initialize the unknown block to a value other than zero to force the equations to converge. To suppress the convergence warnings when solving an implicit system with nonlinear dynamics, activate Suppress Convergence Warnings.
User Defined: When User Defined is activated, Embed uses VSOLVER.DLL in your current directory to solve the equation. For information on creating a custom solver, see Creating custom implicit solvers.