Natural Convection in a Concentric Annulus
In this application, AcuSolve is used to simulate natural convection in the annular space between a heated inner pipe and an outer concentric pipe. AcuSolve results are compared with experimental results adapted from Kuehn and Goldstein (1978). The close agreement of AcuSolve results with experimental results validates the ability of AcuSolve to model cases with flow induced by natural convection.
Problem Description
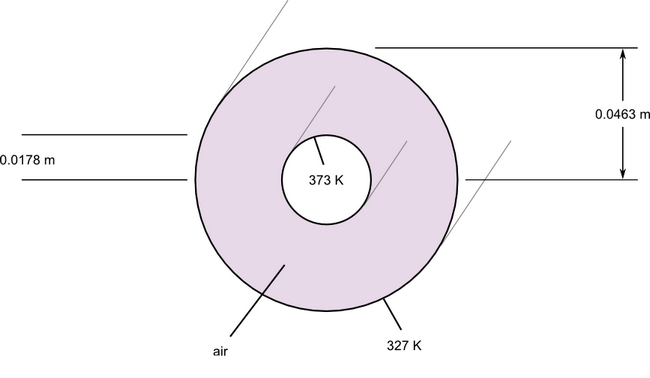
Figure 1. Critical Dimensions and Parameters for Simulating Natural Convection in a Concentric Annulus
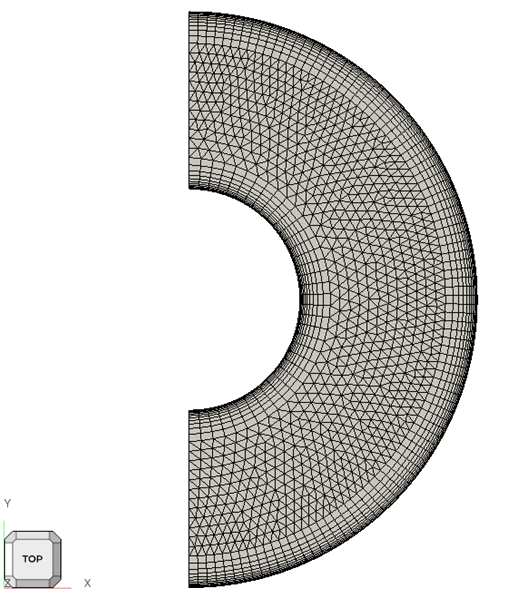
Figure 2. Mesh (Half of a Concentric Annulus) used for Simulating Natural Convection in a Concentric Annulus
AcuSolve Results
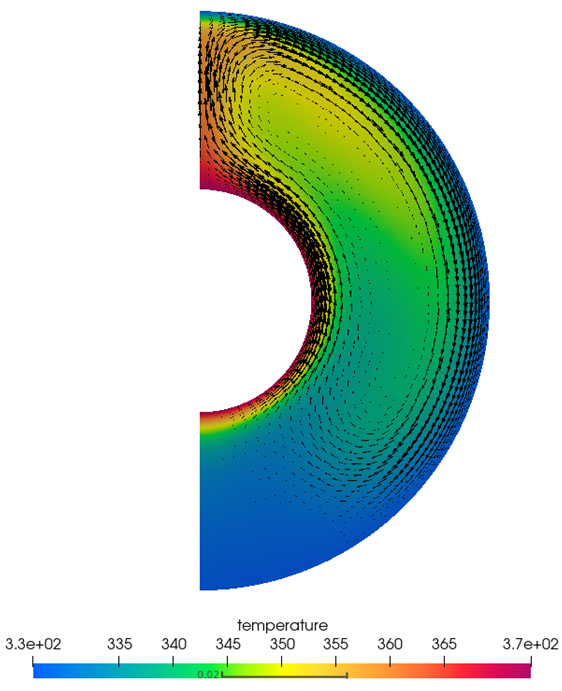
Figure 3. Temperature Contours and Velocity Vectors
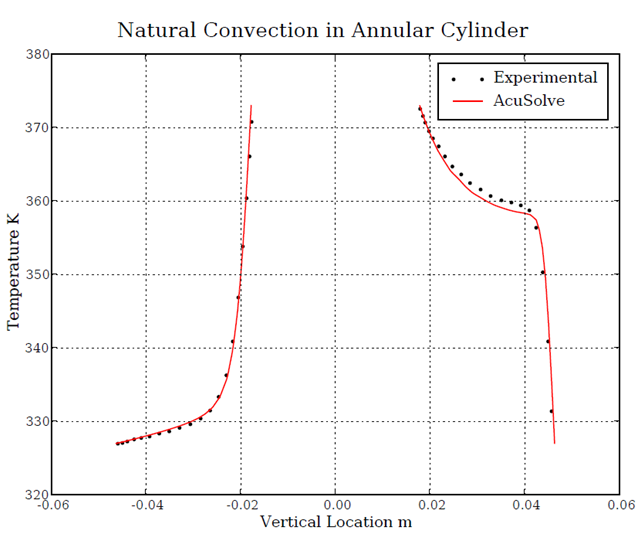
Figure 4. Temperature as a Function of Distance From the Center of the Inner Cylinder
Summary
The AcuSolve solution compares well with analytical results for natural convection in a concentric annulus. In this application, flow is driven by a decrease in density as air is heated. The local variations in density result in the higher density fluid sinking to the bottom of the annulus while the lower density fluid rises to the top. This transfer of momentum is a continuous process which results in the convective currents that are visible in the solution. The AcuSolve temperature results compare very closely with the experimental results.
Simulation Settings for Natural Convection in a Concentric Annulus
HyperWorks CFD database file: <your working directory>\annulus_heat\annulus_heat.hm
Global
- Problem Description
- Analysis type - Steady State
- Abs. pressure offset - 101325.0 N/m2
- Temperature equation - Advective Diffusive
- Turbulence equation - Laminar
- Gravitational acceleration - { 0, -9.80665, 0 }
- Auto Solution Strategy
- Relaxation factor - 0.2
- Flow - On
- Temperature - On
- Material Model
- Air
- Type - Boussinesq
- Density - 1.225 kg/m3
- Expansivity - 0.0034722 1/K
- Reference temperature - 288 K
- Isothermal compressibility - 0.0 m2/N
- Viscosity - 2.081e-5 kg/m-sec
Model
- Air
- Volumes
- Fluid
- Element Set
- Material model - Air
- Element Set
- Surfaces
- ID
- Simple Boundary Condition
- Type - Wall
- Temperature BC type - Value
- Temperature - 373.0 K
- Simple Boundary Condition
- Max_Z
- Simple Boundary Condition
- Type - Symmetry
- Min_Z
- Simple Boundary Condition
- Type - Symmetry
- OD
- Simple Boundary Condition
- Type - Wall
- Temperature BC type - Value
- Temperature - 327.0 K
- Simple Boundary Condition
- Symmetry
- Simple Boundary Condition
- Type - Symmetry
- ID
- Nodes
- Node 1
- Pressure
- Type - Zero
- Pressure
- Node 1
- Fluid
References
T.H. Kuehn and R. J. Goldstein. "An Experimental Study of Natural Convection Heat Transfer in Concentric and Eccentric Horizontal Cylindrical Annuli". Journal of Heat Transfer 100:635-640. 1978.