Supersonic Flow Through a Converging-Diverging Nozzle
In this application, AcuSolve is used to simulate the high-speed turbulent flow in a converging and then diverging nozzle. The flow within the nozzle enters as subsonic, reaches sonic at the throat and shortly after develops a normal shock. AcuSolve results are compared with experimental results adapted from Bogar and Sajben (1983). The close agreement of AcuSolve results to experimental measurements validates the ability of AcuSolve to simulate internal supersonic flows where normal shocks are present.
Problem Description
The problem consists of a converging and then diverging nozzle represented as an extruded planar surface, as shown in the image below, which is not drawn to scale. The length of the domain is 0.213 m with a throat height of 0.044 m. The stagnation pressure and static temperature are constrained at the inlet to 135,000 Pa and 265.98 K, respectively. The static pressure is defined using the outflow boundary condition, where Pstatic=97216.08 Pa. The flow in the diffuser has an inlet Reynolds number of 6.5x105. The upper and lower walls are set to no-slip and the side walls are set to slip, while the exterior walls are specified to be adiabatic. Images of the numerical mesh are shown below.
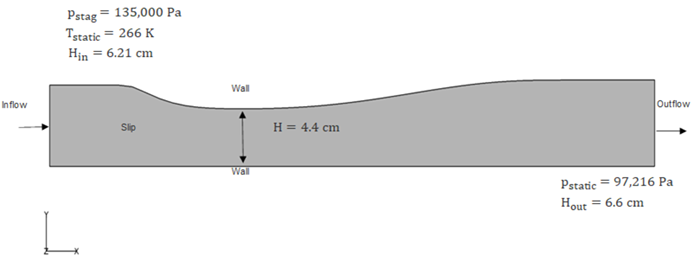
Figure 1. Parameters for Simulating Compressible Flow within a Converging-Diverging Nozzle

Figure 2. Mesh used for Simulating Compressible Flow in a Converging-Diverging Nozzle
AcuSolve Results
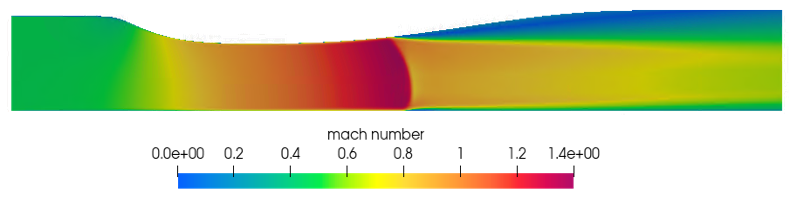
Figure 3. Contours of Mach Number within a Converging-Diverging Nozzle
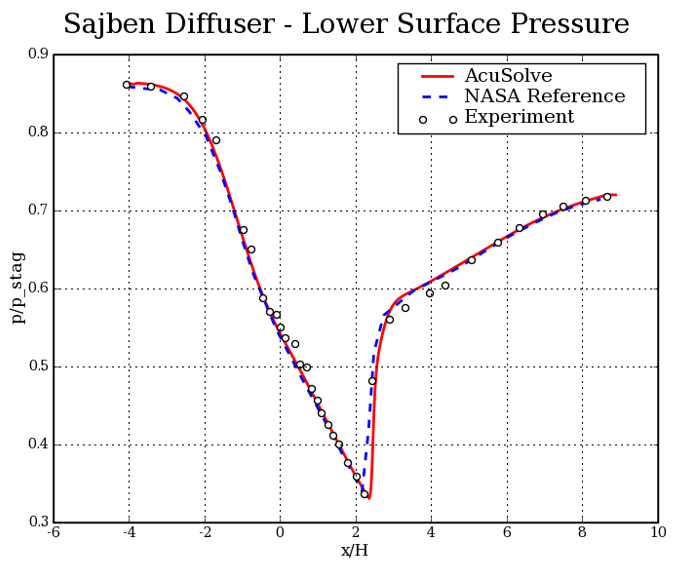
Figure 4. Normalized Pressure Versus Normalized Distance in Comparison to NASA Reference and Experimental Results
Summary
The AcuSolve solution compares well with experimental and numerical results for the described simulation. In this application, compressibility effects are accounted for using the coupled compressible flow solver with the ideal gas material definition. The thermal and momentum exchange within the nozzle is computed with AcuSolve using the compressible Navier-Stokes solver with the Spalart-Allmaras turbulence model. The experimental values of pressure are presented with the corresponding AcuSolve results and show good agreement, validating the ability to solve compressible cases with the presence of normal shocks. The results indicate that AcuSolve is able to properly predict the peak pressure magnitude and location within the diffuser while maintaining the normal shock when the time-step is selected to result in a maximum CFL of approximately 30.
Simulation Settings for Supersonic Flow Through a Converging-Diverging Nozzle
HyperWorks CFD database file: <your working directory>\diffuser_compressible\diffuser_compressible.hm
Global
- Problem Description
- Flow – Compressible Navier Stokes
- Analysis type – Transient
- Turbulence equation – SA
- Temperature equation – Advective Diffusive
- Auto Solution Strategy
- Initial time increment – 4.0E-6
- Final time – 0.025 sec
- Convergence Tolerance – 0.001 sec
- Relaxation factor – 0.5
- Material Model
- Air-Ideal Gas
- Type – Ideal_Gas
- Viscosity – 1.781e-05 kg/m-sec
- Specific Heat – 1005 J/kg-K
- Conductivity – 0.02521 W/m-K
- Gas Constant – 287.058 J/kg-K
- Air-Ideal Gas
Model
- Volumes
- Fluid
- Material – Air-Ideal Gas
- Fluid
- Surfaces
- Inflow
- Simple Boundary Condition – Inflow
- Inflow type – Stagnation Pressure
- Stagnation Pressure – 135000.0 N/m2
- Turbulence_input_type – Direct
- Eddy Viscosity – 1e-6 m2/s
- Temperature – 265.98 K
- Outflow
- Simple Boundary Condition – Outflow
- Pressure – 97216.08 N/m2
- Wall_1
- Simple Boundary Condition – Wall
- Type – auto_wall
- Wall_2
- Simple Boundary Condition – Wall
- Type – auto_wall
- Slip_1
- Simple Boundary Condition – Slip
- Slip_2
- Simple Boundary Condition – Slip
- Inflow
References
Bogar, T. J., Sajben, M., and Kroutil, J. C. (1983) "Characteristic Frequencies of Transonic Diffuser Flow Oscillations," AIAA Journal, Vol. 21, No. 9, pp. 1232-1240.
Mohler, S.R., "Wind-US Unstructured Flow Solutions for a Transonic Diffuser," NASA CR-2005-213417, January 2005.