HS-3000: Fit Method Comparison - Approximation on the Arm Model
Learn how to create approximations for the output responses of the arm example introduced in tutorial, and review the differences between different Fit methods.
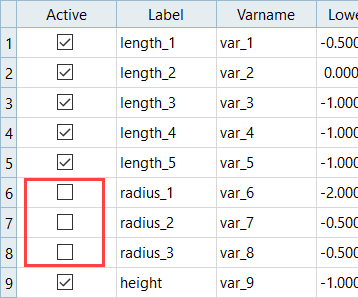
In HS-2000: DOE Method Comparison: Arm Model Study, you learned that instead of using the nine input variables, you could continue additional studies just as effectively with six shapes since the others did not have a great influence on the output responses. This will save computational effort.
- Length1: Lower Bound = -0.5, Initial Bound = 0.0, Upper Bound = 2.0
- Length2: Lower Bound = 0.0, Initial Bound = 0.0, Upper Bound = 2.0
- Length3: Lower Bound = -1.0, Initial Bound = 0.0, Upper Bound = 1.0
- Length4: Lower Bound = -1.0, Initial Bound = 0.0, Upper Bound = 1.0
- Length5: Lower Bound = -1.0, Initial Bound = 0.0, Upper Bound = 1.0
- Height: Lower Bound = -1.0, Initial Bound = 0.0, Upper Bound = 1.0
Run MELS DOE Study
In this step you will create a Modified Extensible Lattice Sequence (MELS) DOE. You will use this matrix to create the Fits for both output responses.
MELS is a space filling DOE designed to equally spread out points in a space by minimizing clumps and empty spaces. The minimal required number of points to create a second order polynomial with N variables is 1.1*(N + 1)*(N + 2)/2.
In order to create the approximations to be used as surrogate models, you must perform specific DOEs that will serve as the input matrix. You will need to run a DOE suitable to be used in response surface creation, such as MELS.
Optional: Run DOE with Less Runs
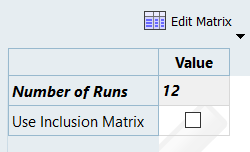
In this step you will create an optional second DOE with less number of runs to be used as a Validation matrix in the Fit approach.
In this tutorial, you will use the Hammersley method to create the Validation matrix.
-
Add a DOE.
-
Define specifications.
-
Evaluate tasks.
- Go to the step.
- Click Evaluate Tasks.
Run Fits
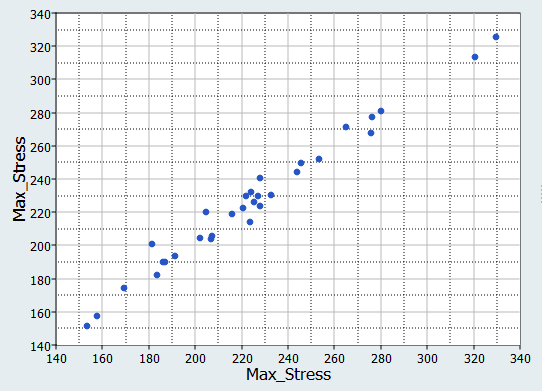
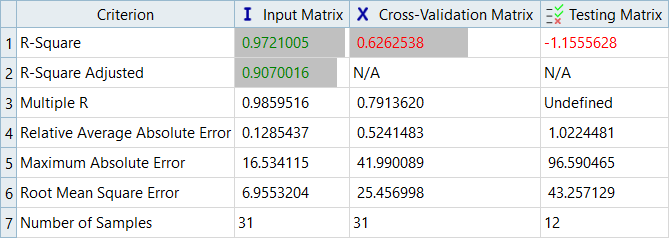
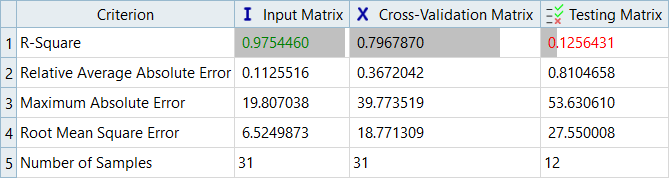
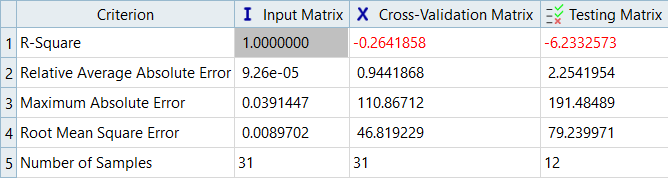
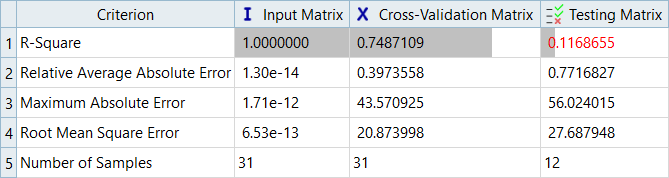
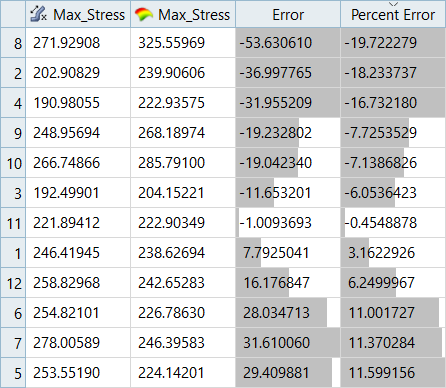
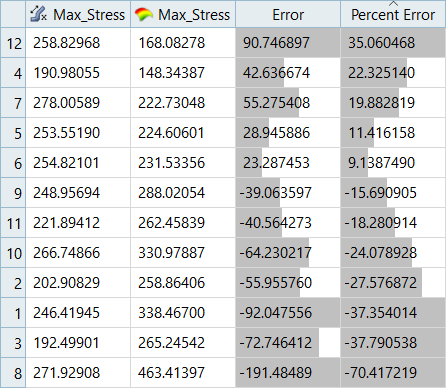
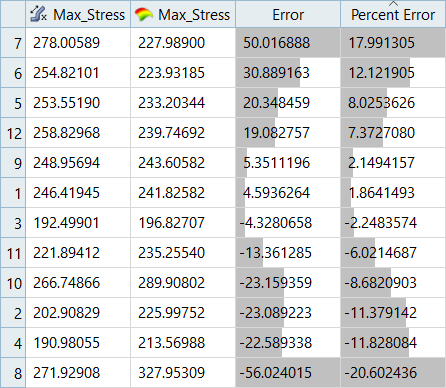
In this step you will use the 31 runs from the MELS DOE as an Input matrix and the 12 runs from the Hammersley DOE as a Validation matrix to create four Fits using Least Square Regression (LSR), Moving Least Square Method (MLSM), HyperKriging (HK), and Radial Basis Function (RBF).
Fit Comparison
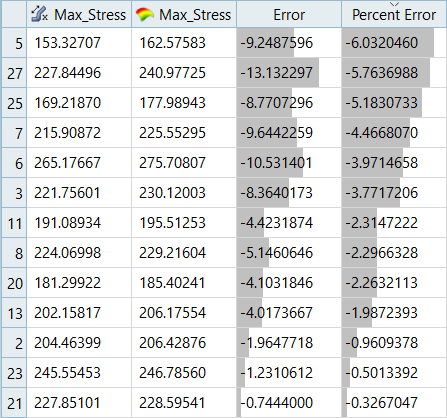
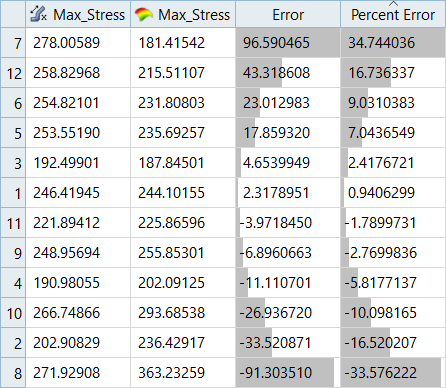
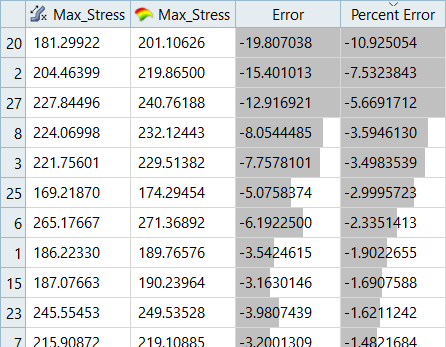
Overview of the max percent of errors for Input and Testing matrices.
| LSR (Interaction Regression Model) | MLSM | HK | RBF | |
|---|---|---|---|---|
| Max_Disp | -1.18% | -2.79% | - | - |
| Max_Stress | -6.72% | -10.92% | - | - |
| LSR (Interaction Regression Model) | MLSM | HK | RBF | |
|---|---|---|---|---|
| Max_Disp | 7.26% | -3.00% | 9.57% | -2.45% |
| Max_Stress | 34.74% | -19.72% | 35.06% | 17.99% |
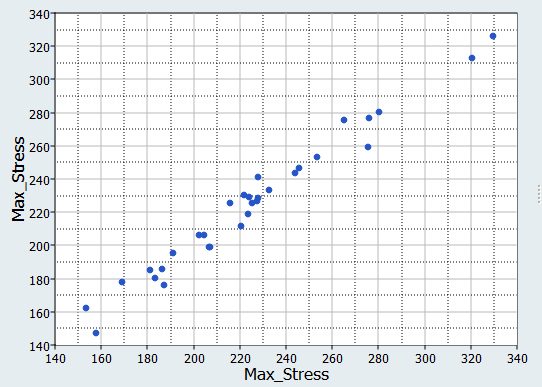
It can be seen that the percent of errors for Max_Disp are smaller than Max_Stress. These results indicate the Fit approach works well for Max_Disp, but is not very efficient for Max_Stress.
Figure 17.