HS-4200: Material Calibration Using System Identification
Learn a method for characterizing parameters of a RADIOSS material law used for modeling elasto-plastic material.
The characterization of a ductile aluminum alloy is studied. A RADIOSS simulation is performed to replicate an experimental tensile test. The parameters of the material law are determined to fit the experimental results.
HS-1506: Material Calibration with a Curve Difference Integral provides an alternative method to setup this problem using a HyperMath or Python function to measure the difference between two curves.
HS-1507: Material Calibration with Area Tool in Data Source provides an alternative method to set up this problem using the Area tool.
Model Definition
A quarter of a standard tensile test specimen is modeled using symmetry conditions. A traction is applied to a specimen via an imposed velocity at the left-end.

Figure 1. Geometry of the Tensile Specimen (One Quarter of the Specimen is Modeled)
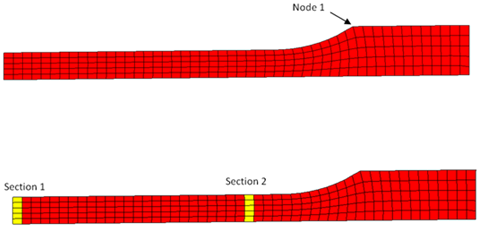
Figure 2. Sections of Node Saved for Time History
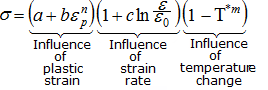
- Stress level
- Plastic strain
- Yield Stress
- Hardening modulus
- Hardening exponent
- Strain rate coefficient
- Strain rate
- Reference strain rate
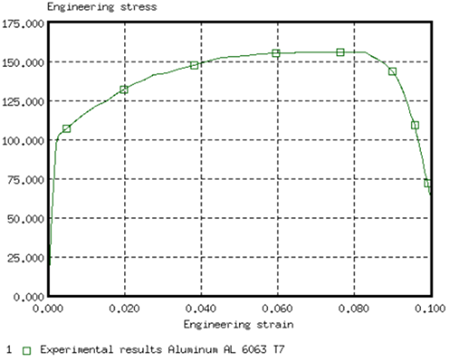
Figure 3. Engineering Stress Versus Engineering Strain Curve (Experimental Data)
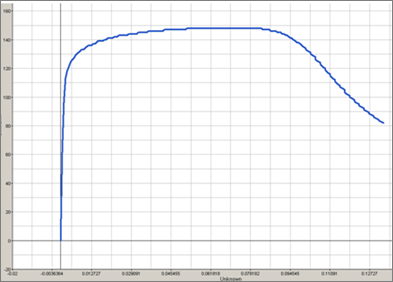
Figure 4. Engineering Stress Versus Strain Curve (Simulation Results)
Create Base Input Template
In this step, create the base input template in HyperStudy or use the base input template in the study directory.
Perform the Study Setup
Perform Nominal Run
Create and Evaluate Output Responses
In this step, you will compare RADIOSS stress-strain curve to the experimental data.
- Difference between experimental stress and RADIOSS at Strain equal 0.02 (1)
- Difference between experimental strain and RADIOSS at Necking point (2)
- Difference between experimental stress and RADIOSS at Necking point (3)
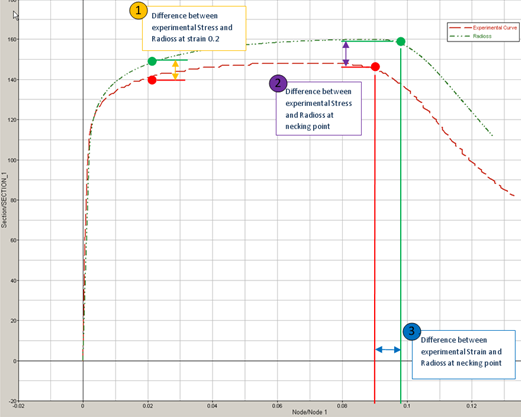
Figure 10.
- Go to the Define Output Responses step.
-
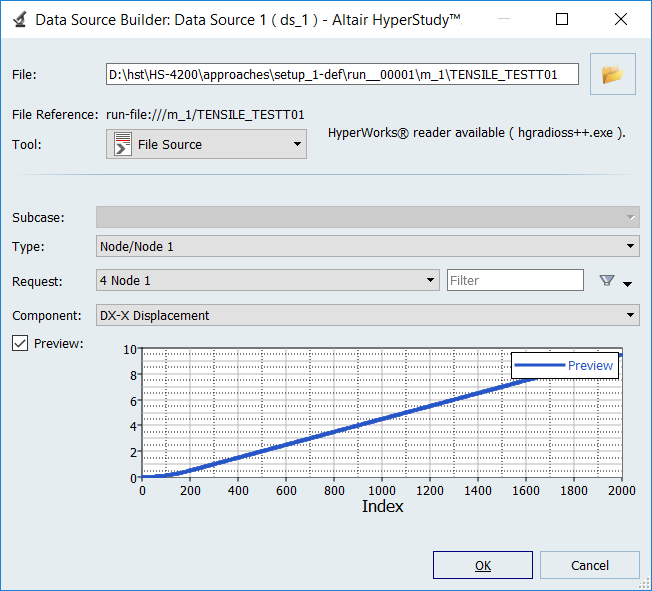
Create a data source labeled Disp_sim.
-
Repeat step 2 to
create a second data source labeled Force_sim, making the
following changes during the process:
- Set Type to Section/SECTION_2.
- Set Request to 2 section 1.
- Set Component to FT-Resultant Tangent Force.
-
Create three output responses.
-
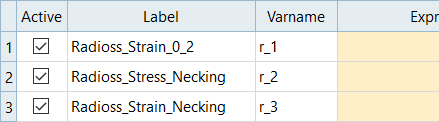
Define the Radioss_Strain_0_2 output response.
-
Define the Radioss_Stress_Necking output response.
-
Define the Radioss_Strain_Necking output response.
- Click Evaluate to extract the response values.
 .
.
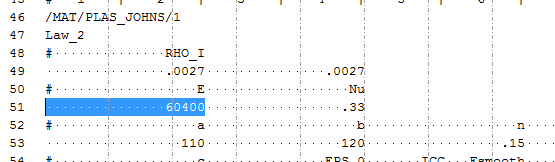
 .
.