絶対節点座標法

絶対節点座標法（ANCF： Absolute Nodal Coordinate Formulation）は、適用される荷重下で変形することができる、1次元、2次元、および3次元における弾性コンポーネントの有限要素ベースの表現です。これは、マルチボディシステムで非線形弾性要素（NLFE： Non Linear Flexible Element）コンポーネントをモデル化できるようにする定式化です。

このような弾性コンポーネントを使用して、可変形ボディの動的な運動を表現できます。完全に非線形な定式化によって、この手法は、その要素内の大きな変形と大規模な回転を扱うことができます。MotionSolveで実装されているANCFを使用すると、ゴムなどの超弾性材料をはじめとする、非線形特性を備えた材料をモデル化することもできます。

BEAM要素

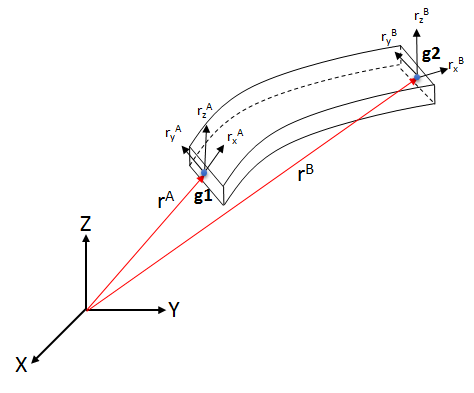
例えば、ANCFによってモデリングされたBEAM12要素を考えます。このようなBEAM要素は、2つの節点（1つは要素の始点（g1）、もう1つは終点（g2）に位置する）によって定義されるという点で、LINE要素と見なすことができます。これは、図 1に示すとおりです。


図 1. ANCFによるBEAM12要素
従来の有限要素とは異なり、完全にパラメータ化された要素（BEAM12要素のように）の各節点は12の座標によって表されます。これらは次のとおりです。
3D空間内の節点の位置。

r _ = x i ^ + y j ^ + z k ^

X方向の勾配ベクトル。
r → x = ( ∂ r → ∂ x ) x   i ^ + ( ∂ r → ∂ x ) y + j ^ ( ∂ r → ∂ x ) z   k ^
Y方向の勾配ベクトル。
r → y = ( ∂ r → ∂ x ) x   i ^ + ( ∂ r → ∂ x ) y + j ^ ( ∂ r → ∂ x ) z   k ^
Z方向の勾配ベクトル。
r → z = ( ∂ r → ∂ x ) x   i ^ + ( ∂ r → ∂ x ) y + j ^ ( ∂ r → ∂ x ) z   k ^
これらはまとめて、ビームの節点座標と呼ばれます。グリッドの位置は、位置ベクトル r → によって空間内で定義されます。X、Y、Z方向に沿った軸ひずみは、勾配ベクトルの大きさによって定義されます。すなわち、
X方向の軸ひずみの定義
| r → x |
Y方向の軸ひずみの定義
| r → y |
Z方向の軸ひずみの定義
| r → z |
さらに、せん断ひずみはこれらのベクトル間の角度によって定義されます。以下からわかるように、BEAM12の節点の自由度は12です：
節点の自由度
X軸に沿った節点の剛体並進
Y軸に沿った節点の剛体並進
Z軸に沿った節点の剛体並進
X軸を中心とした節点の剛体回転
Y軸を中心とした節点の剛体回転
Z軸を中心とした節点の剛体回転
X軸に沿った変形（軸ひずみ）
Y軸に沿った変形（軸ひずみ）
Z軸に沿った変形（軸ひずみ）
XY平面における変形（せん断ひずみ）
YZ平面における変形（せん断ひずみ）
ZX平面における変形（せん断ひずみ）
完全にパラメータ化されているBEAM12要素は、軸荷重、せん断荷重、ねじり荷重､および曲げ荷重に抵抗することができます。したがって、図 2に示すように、複数のBEAM12要素を使用してビームコンポーネントをモデリングできます。


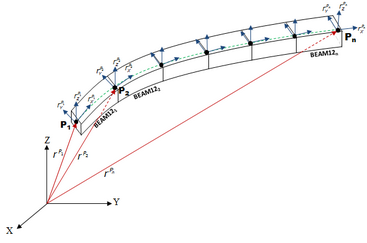
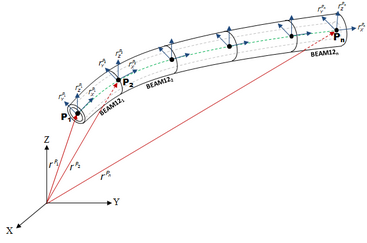図 2. 複数のBEAM12要素を使用してモデリングされたビーム（矩形と管の断面を使用）

BEAM12要素の形状プロパティはPBEAML要素を使用して指定できます。PBEAML要素を使用すると、関連する寸法とともにビームの断面を定義できます。形状プロパティに加えて、BEAM12要素の材料プロパティも指定する必要があります。BEAM12要素は、材料モデルとして線形弾性モデルと超弾性モデルをサポートしています。詳細については、ドキュメント内の各種材料プロパティ要素をご参照ください。

CABLE要素

MotionSolveでサポートされている2種類目のLINE要素はCABLE要素です。このようなCABLE要素は、2つの節点（1つは要素の始点（g1）、もう1つは終点（g2）に位置する）によって定義されるという点で、LINE要素と見なすことができます。これは、図 3に示すとおりです。



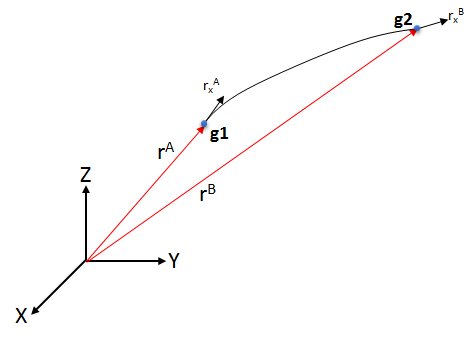
図 3. ANCFによるCABLE要素
CABLE要素の各節点は６個の座標のみで表されます。これらは次のとおりです。
3D空間内の節点の位置。
r → = x i ^ + y j ^ + z k ^
X方向の勾配ベクトル。
r → x = ( ∂ r → ∂ x ) x   i ^ + ( ∂ r → ∂ x ) y + j ^ ( ∂ r → ∂ x ) z   k ^
これらはまとめて、ケーブルの節点座標と呼ばれます。節点の位置は、位置ベクトル r → によって空間内で定義されます。X方向に沿った軸ひずみは、勾配ベクトルの大きさによって定義されます。すなわち、
X方向の軸ひずみの定義
| r → x |

この要素の構成に基づいて、この要素が軸荷重と曲げ荷重のみに抵抗することができることは容易にわかります。この要素の断面は一定であると見なされ、荷重の増大に伴って変形することはありません。

CABLEの節点の自由度は9です：
節点の自由度
X軸に沿った節点の剛体並進
Y軸に沿った節点の剛体並進
Z軸に沿った節点の剛体並進
X軸を中心とした節点の剛体回転
Y軸を中心とした節点の剛体回転
Z軸を中心とした節点の剛体回転
X軸に沿った変形（軸ひずみ）
Y軸に沿った変形（軸ひずみ）
Z軸に沿った変形（軸ひずみ）

したがって、図 4に示すように、複数のCABLE要素を使用してワイヤーまたはケーブルのコンポーネントをモデリングできます。



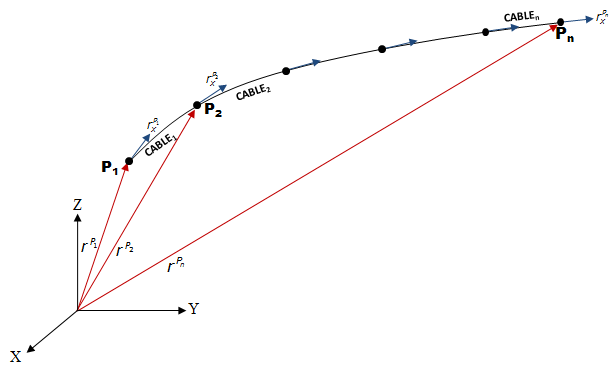
図 4. 複数のCABLE要素を使用してモデリングされたワイヤー / ケーブル

CABLE要素の形状プロパティはPCABLE要素を使用して指定できます。PCABLE要素を使用すると、ケーブルの断面領域、領域のモーメント、および他のポスト処理フラグを定義できます。形状プロパティに加えて、CABLE要素の材料プロパティも指定する必要があります。CABLE要素は、線形弾性材料モデルのみをサポートしています。詳細については、ドキュメントをご参照ください。

BEAM要素とCABLE要素の材料の指定

ANCFの最新の実装では、さまざまな材料モデルがサポートされています。MotionSolveでANCFによってサポートされている材料タイプは次のとおりです：
材料タイプ
要素タイプ
線形弾性（連続体力学および弾性曲線アプローチ）
BEAM12とCABLE
超弾性（Neo-Hookean、Mooney Rivlin、およびYeoh）
BEAM12のみ
線形弾性材料は一般に次の特性を示します：
  • 材料は可逆的に変形します。すなわち、荷重が取り除かれるとすぐに、材料は元の形状に戻ります。
  • 応力はひずみの線形関数です。
  • ひずみは荷重速度に依存しません。

線形弾性材料モデルは、ヤング率、ポアソン比、および材料密度という3つのパラメータによって定義されます。このモデルを使用して、ほとんどの金属とプラスチックを閾値荷重に達するレベルまでモデリングできます。この閾値荷重を超えると、これらの金属やプラスチックは塑性変形を示し始め、最終的に降伏します。

これら3つの材料パラメータの値は一般に、材料を実験室で試験することによって得られます。ただし、この材料モデルは単純であるため、これらの値は教科書や工学便覧から簡単に入手できる場合があります。

超弾性材料モデルは主に以下の点で線形弾性材料モデルと異なります：
  • 材料内の応力はひずみの線形関数ではありません。
  • このタイプの材料モデルを使用して、最大200％にも上る大きなひずみをモデリングします。

超弾性材料モデルは一般に、エラストマー（ゴムなど）、ポリマー、フォーム、生体材料（筋肉など）などをモデリングするために使用されます。このような材料をモデリングするために、ひずみエネルギー密度関数を利用する構成則が使用されます。ひずみエネルギー密度は、任意の材料の応力-ひずみ曲線が適用される領域であると考えることができます。ひずみエネルギー密度関数の定式化の詳細については、リファレンスマニュアルをご参照ください。

MotionSolve内の現時点でのANCF実装では、このような3つの構成則を使用できます：
材料則のタイプ
材料の定義に使用されるパラメータ
Neo-Hookean材料則
μ （せん断弾性係数）と密度
υ （ポアソン比）
ρ （密度）
Mooney-Rivlin材料則
μ 01 （材料の定数）
μ 10 （材料の定数）
υ （ポアソン比）
ρ （密度）
Yeoh材料則
C 10 （材料の定数）
C 30 （材料の定数）
υ （ポアソン比）
ρ （密度）

せん断弾性係数、ポアソン比、および密度のパラメータは工学便覧や教科書に記載されている可能性がありますが、Mooney-Rivlin材料則とYeoh材料則の材料定数は実験室での試験を通じて算出されます。一般に、単軸、二軸、および平面試験を実施することで、さまざまな作用点での材料内の応力とひずみが測定されます。その後、このデータにより応力とひずみの間の非線形関係を表す曲線が近似されます。図 5に、単軸試験を通じて得られたこれら3つの材料則の一般的な応力-ひずみ関係を示します。

注: 超弾性材料は、圧縮荷重や引張荷重のモデリング用です。これらの構成モデルを使用している場合は、純粋な曲げを伴う用途では正確な結果が得られない可能性があります。


図 5. 超弾性材料則の工学的応力と工学的ひずみの関係

どの材料モデルを使用するべきか

超弾性材料内で予想されるひずみと用途に応じて、選択する材料則は変わります。小さなひずみ（10％未満）が予想される用途では、線形弾性材料の使用で十分かもしれません。大きなひずみが予想される場合（ゴムのモデリング時など）は、3つの超弾性モデルのうち最もシンプルなNeo-Hookeanモデルを最初に使用することが推奨されます。

試験データが簡単に得られる場合は、YeohモデルまたはMooney-Rivlinモデルを使用してもかまいません。これら2つのモデルのうちどちらを選択するかは、目的のひずみ / 伸張範囲でこれらの材料則と試験データの間でどれだけ良好な曲線近似が得られるかによって異なります。

MotionViewでは、3つすべての超弾性材料モデルについてサンプルの係数値群が用意されています。MotionViewではユーザー独自の材料定数を使用することもできます。