GTCMAT

使用

GTCMATは、通常、REQSUBユーザーサブルーチンから呼び出されます。

フォーマット

Fortranの呼出し構文

CALL GTCMAT (NM, MKID, NC, CMAT, ISTAT)

C/C++の呼出し構文

c_gtcmat(nm, mkid, nc, cmat, istat)

Pythonの呼出し構文

[cmat, istat] = py_gtcmat(mkid)

属性

NM

整数

NM > 0

コンプライアンスマトリクスを計算するREFERENCE_MARKERの数を定義します。

MKID

整数

配列サイズ ≥ NM

コンプライアンスマトリクスを計算するREFERENCE_MARKERのIDが含まれます。

NC

整数

NC > 6* NM

計算されたコンプライアンスマトリクスを含む倍精度配列CMATの行寸法と列寸法を定義します。

出力

CMAT

倍精度

NC * NC

指定されたREFERENCE_MARKERのコンプライアンスマトリクスを含む配列。

ISTAT

整数

GTCMATからの戻りステータス。ISTATの意味は次のとおりです：

ISTAT= 0

正常復帰。コンプライアンスマトリクスが計算されました。

ISTAT= -1

エラー復帰。NM < 0。

ISTAT= -2

エラー復帰。NM > 100。

ISTAT= -3

エラー復帰。NC < 6*NM。

ISTAT= -6

エラー復帰。MKIDが、存在しないREFERENCE_MARKERを参照しています。

ISTAT= -7

エラー復帰。システムの自由度が0です。

ISTAT= -9

エラー復帰。計算中に非正則ヤコビアンマトリクスが出現しました。

ISTAT=-11

エラー復帰。REFERENCE_MARKERのいずれかがGROUND上に存在します。定義により、移動することができません。

ISTAT=-12

エラー復帰。初期静的平衡が実行されませんでした。

ISTAT=-99999

エラー復帰。

例

図 1 （下図）は、円環Aに掛けられた三角形Tを示しています。円環Aは地面に設置されています。Tは3つのブッシュ（B1、B2、およびB3）によってAに結合されています。Tの質量プロパティとB1、B2、およびB3の剛性特性を以下に示します。このテストの目的は、3つのブッシュ位置におけるシステムのコンプライアンスを求めることです。システムは次のようにモデル化されています：

単位	プロパティ	形状
長さ = mm 質量 = Kg 時間 = 秒 力 = ニュートン	Tの質量プロパティ 質量 = 170.1587874 Kg 慣性 = 1.607495985E+007、1.181530722E+007、4.33055212E+006 B1、B2、およびB3における剛性特性： K = 200、200、200 KT = 2.291831181E+005、2.864788976E+005、3.437746771E+005	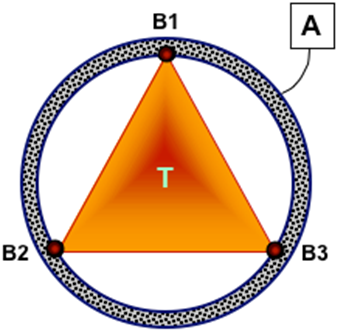図 1. 円環Aに掛けられた三角形T

コンプライアンスマトリクスを計算するために、REQSUBを記述します。REQSUBでは、GTCMATが適切なパラメータを使用して呼び出されます。REQSUBはコンプライアンスマトリクスを取得してそれをファイルに書き込みます。このファイルの内容を以下に示します。

ファイルには、便宜上6x6のブロックに分割された18x18のマトリクスが含まれています。

COMPLIANCE MATRIX
=================
IM = B1 JM = B1
Row Range =  1 -- 6
Col Range =  1 -- 6
    2.78486E-03    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00   -2.79544E-06
    0.00000E+00    1.66667E-03    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00    3.49751E-03    4.57714E-06    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00    4.57711E-06    0.00000E+00    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
   -2.79548E-06    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
IM = B1 JM = B2
Row Range =  1 -- 6
Col Range =  7 --12
    1.10757E-03    8.38643E-04    0.00000E+00    0.00000E+00    0.00000E+00   -2.79544E-06
    0.00000E+00    1.66667E-03    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00    7.51245E-04    4.57714E-06    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00   -2.28855E-06    0.00000E+00    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00    3.51939E-06    0.00000E+00    0.00000E+00    0.00000E+00
    1.39774E-06   -2.09661E-06    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
IM = B1 JM = B3
Row Range =  1 -- 6
Col Range = 13 --18
    1.10757E-03   -8.38643E-04    0.00000E+00    0.00000E+00    0.00000E+00   -2.79543E-06
    0.00000E+00    1.66667E-03    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00    7.51245E-04    4.57714E-06    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00   -2.28855E-06    0.00000E+00    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00   -3.51939E-06    0.00000E+00    0.00000E+00    0.00000E+00
    1.39774E-06    2.09661E-06    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
IM = B2 JM = B1
Row Range =  7 --12
Col Range =  1 -- 6
    1.10757E-03    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00    1.39772E-06
    8.38643E-04    1.66667E-03    0.00000E+00    0.00000E+00    0.00000E+00   -2.09658E-06
    0.00000E+00    0.00000E+00    7.51245E-04   -2.28857E-06    3.51938E-06    0.00000E+00
    0.00000E+00    0.00000E+00    4.57711E-06    0.00000E+00    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
   -2.79548E-06    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
IM = B2 JM = B2
Row Range =  7 --12
Col Range =  7 --12
    1.94621E-03   -4.19322E-04    0.00000E+00    0.00000E+00    0.00000E+00    1.39772E-06
   -4.19322E-04    2.29565E-03    0.00000E+00    0.00000E+00    0.00000E+00   -2.09658E-06
    0.00000E+00    0.00000E+00    3.18019E-03   -2.28857E-06    3.51938E-06    0.00000E+00
    0.00000E+00    0.00000E+00   -2.28855E-06    0.00000E+00    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00    3.51939E-06    0.00000E+00    0.00000E+00    0.00000E+00
    1.39774E-06   -2.09661E-06    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
IM = B2 JM = B3
Row Range =  7 --12
Col Range = 13 --18
    1.94621E-03    4.19322E-04    0.00000E+00    0.00000E+00    0.00000E+00    1.39772E-06
   -4.19322E-04    1.03768E-03    0.00000E+00    0.00000E+00    0.00000E+00   -2.09658E-06
    0.00000E+00    0.00000E+00    1.06856E-03   -2.28857E-06    3.51938E-06    0.00000E+00
    0.00000E+00    0.00000E+00   -2.28855E-06    0.00000E+00    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00   -3.51939E-06    0.00000E+00    0.00000E+00    0.00000E+00
    1.39774E-06    2.09661E-06    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
IM = B3 JM = B1
Row Range = 13 --18
Col Range =  1 -- 6
    1.10757E-03    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00    1.39772E-06
   -8.38643E-04    1.66667E-03    0.00000E+00    0.00000E+00    0.00000E+00    2.09658E-06
    0.00000E+00    0.00000E+00    7.51245E-04   -2.28857E-06   -3.51938E-06    0.00000E+00
    0.00000E+00    0.00000E+00    4.57711E-06    0.00000E+00    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
   -2.79548E-06    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
IM = B3 JM = B2
Row Range = 13 --18
Col Range =  7 --12
    1.94621E-03   -4.19322E-04    0.00000E+00    0.00000E+00    0.00000E+00    1.39772E-06
    4.19322E-04    1.03768E-03    0.00000E+00    0.00000E+00    0.00000E+00    2.09658E-06
    0.00000E+00    0.00000E+00    1.06856E-03   -2.28857E-06   -3.51938E-06    0.00000E+00
    0.00000E+00    0.00000E+00   -2.28855E-06    0.00000E+00    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00    3.51939E-06    0.00000E+00    0.00000E+00    0.00000E+00
    1.39774E-06   -2.09661E-06    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00
IM = B3 JM = B3
Row Range = 13 --18
Col Range = 13 --18
    1.94621E-03    4.19322E-04    0.00000E+00    0.00000E+00    0.00000E+00    1.39772E-06
    4.19322E-04    2.29565E-03    0.00000E+00    0.00000E+00    0.00000E+00    2.09658E-06
    0.00000E+00    0.00000E+00    3.18019E-03   -2.28857E-06   -3.51938E-06    0.00000E+00
    0.00000E+00    0.00000E+00   -2.28855E-06    0.00000E+00    0.00000E+00    0.00000E+00
    0.00000E+00    0.00000E+00   -3.51939E-06    0.00000E+00    0.00000E+00    0.00000E+00
    1.39774E-06    2.09661E-06    0.00000E+00    0.00000E+00    0.00000E+00    0.00000E+00

18x18のマトリクスは、下の図のように、6x6のブロックに分けられています。互いに入れ替えられているブロックに同じ色が付けられています。

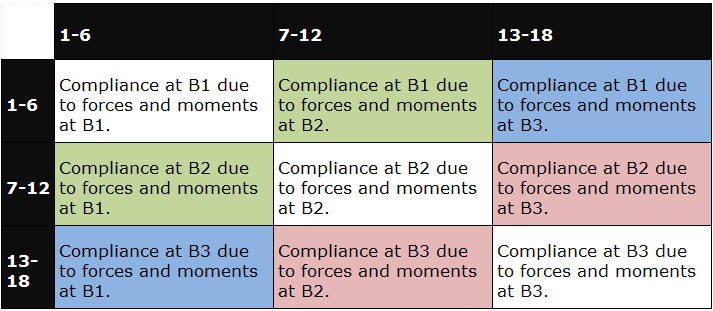
図 2. コンプライアンスマトリクスCMATのブロック定義。

コメント

1. GTCMATは、ユーザー作成サブルーチンから呼び出されます。GTCMATは、呼び出し元のユーザーサブルーチンでIFLAG = TRUEと指定されているときに呼び出す必要があります。
2. コンプライアンスマトリクスは、静的平衡状態で計算されたシステムの伝達関数です。伝達関数には入力と出力が必要です。コンプライアンスマトリクスの計算では、これらが次のように定義されます：
   • $U$ は、線形化されたシステムへの入力を表します。これはサイズが6*NMの配列です。各成分 $U(i)$ は、“NM”個のREFERENCE_MARKERにおける6つの方向のいずれかで作用する力またはトルクです。
   • $Y$ は、線形化されたシステムからの出力を表します。これは次元が6*NMの配列です。各成分 $Y(j)$ は、“NM”個のREFERENCE_MARKERにおける6つの方向のいずれかで作用する並進または回転変位です。
3. 静的平衡状態では、入力が $U$ で出力が $Y$ のシステムの伝達関数を次のように表すことができます：
   (1)

   $$\left[ComplianceMatrix\right]=\frac{Y\left(s=0\right)}{U\left(s=0\right)}=C{A}^{-1}B+D$$
   上記方程式内の数量は、次のように定義されます：

   • $s=\sigma +j\omega$ は、ラプラス領域変数を表します。 $\sigma$ は減衰、 $\omega$ は振動状態の周波数で、 $j=\sqrt{-1}$ です。
   • $\left[A\right],\left[B\right],\left[C\right],\left[D\right]$ は、適切な次元の定数値マトリクスです。これらは、作用点におけるシステムの状態マトリクスと呼ばれています。
   • $\left[ComplianceMatrix\right]$ は、6NM x 6NMマトリクスです。
4. システム内の、注目するi番目のREFERENCE_MARKER、Iでは、6つの入力が次のように定義されます： $U(i)$ $Y(j)$ $Y$
   • $U\left[1\right]:$ 全体座標系のx軸に沿って作用するIの原点における単位力。
   • $U\left[2\right]:$ 全体座標系のy軸に沿って作用するIの原点における単位力。
   • $U\left[3\right]:$ 全体座標系のz軸に沿って作用するIの原点における単位力。
   • $U\left[4\right]:$ 全体座標系のx軸周りに作用するIでの単位トルク。
   • $U\left[5\right]:$ 全体座標系のy軸周りに作用するIでの単位トルク。
   • $U\left[6\right]:$ 全体座標系のz軸周りに作用するIでの単位トルク。
5. システム内の、注目するj番目のREFERENCE_MARKER、Jでは、出力が次のように定義されます：
   • $Y\left[1,k\right]:$ 入力 $U\left(k\right)$ による、全体座標系のx軸に沿って測定されたJの原点の並進変位。
   • $Y\left[2,k\right]:$ 入力 $U\left(k\right)$ による、全体座標系のy軸に沿って測定されたJの原点の並進変位。
   • $Y\left[3,k\right]$ 入力 $U\left(k\right)$ による、全体座標系のz軸に沿って測定されたJの原点の並進変位。
   • $Y\left[4,k\right]:$ 全体座標系のx軸周りに測定された、入力 $U\left(k\right)$ による、Jの回転の小角度近似。
   • $Y\left[5,k\right]:$ 全体座標系のy軸周りに測定された、入力 $U\left(k\right)$ による、Jの回転の小角度近似。
   • $Y\left[6,k\right]:$ 全体座標系のy軸周りに測定された、入力 $U\left(k\right)$ による、Jの回転の小角度近似。
6. コンプライアンスマトリクスの計算は、特に、サスペンションの弾性運動学的評価に有益です。複数のサスペンション設計要素をコンプライアンスマトリクス内の数量の関数として表現できます。

   例えば、鉛直方向のホイールレートは、ホイール中心に適用された鉛直荷重による、ホイール中心における鉛直変位量の逆数として定義されます。

   サスペンションホイール中心に配置された2つのマーカー間のコンプライアンスマトリクスが計算済みであると仮定すると、鉛直ホイールレートが次のように表されることは一目瞭然です：

   • 左鉛直ホイールレート = $1/\left(C\left[3,3\right]+C\left[3,9\right]\right)$
   • 右鉛直ホイールレート = $1/\left(C\left[9,3\right]+\text{C}\left[9,9\right]\right)$

     ここで、コンプライアンスマトリクスに入力されるさまざまな項は次のとおりです：

   • $C\left[3,3\right]$ = 左ホイールに適用された単位鉛直力による左ホイールの鉛直変位。
   • $C\left[3,9\right]$ = 右ホイールに適用された単位鉛直力による左ホイールの鉛直変位。
   • $C\left[9,3\right]$ = 左ホイールに適用された単位鉛直力による右ホイールの鉛直変位。
   • $C\left[9,9\right]$ = 右ホイールに適用された単位鉛直力による右ホイールの鉛直変位。
7. 代表的なコンプライアンスマトリクスの用途には、他にスプリングとダンパのモーション比率の計算もあります。スプリングのモーション比率は、スプリングの軸に沿った相対変位と、上側と下側のスプリングシート間に適用された相対荷重間の比率として定義されます。この量は、下側のスプリングシートに配置されたマーカーと上側のスプリングシートに配置されたマーカー間のコンプライアンスマトリクスを計算することによって簡単に取得できます。