システムには複数の目的を満たすことが求められます。これらの問題には、互いに少しずつ異なるアプローチが必要です。
多目的最適化は、以下のように規定できます:
| 最小化 |
|
(目的関数) |
| 適用条件 |
|
(不等式の制約条件) |
| |
|
(等式の制約条件) (設計の制限値)
|
コスト関数と制約関数の各関数
は、次の形式をとると想定されます:
MotionSolveでは、コスト関数を次のように再定義することで、多目的問題が単一目的の問題に変換されます:
| 最小化: |
|
(目的関数) |
| 適用条件: |
|
(不等式の制約条件) (等式の制約条件)
(設計の制限値)
|
は、さまざまな目的の相対的な重要度を反映した重み付けのセットです。
例1
- 設計目標
- 設計目標は、運動学的SLAサスペンションを考慮し、サスペンションのハードポイントを変更して目的のライド挙動を得ることです。
図 1.
ライド挙動の特性は、次の6つの目的で記述できます:
- 設計位置のライドステア = -4°/m
- フルジャウンス位置のライドステア = -4°/m
- 設計位置のライドキャンバー = +5°/m
- フルジャウンス位置のライドキャンバー = +5°/m
- 設計位置のライドキャスター = -8°/m
- フルジャウンス位置のライドキャスター = -8°/m
ライドステア =
ライドキャンバー =
ライドキャスター =
- 設計変数
- サスペンションの中でさまざまなハードポイントの位置を設計変数として使用できます。この問題には、26個の設計変数があります。
| アッパーコントロールアームのインボードのハードポイント(前後)XYZ |
(6個の設計変数) |
| ロアーコントロールアームのインボードのハードポイント(前後)XYZ |
(6個の設計変数) |
| アッパーボールジョイントのハードポイントXYZ |
(3個の設計変数) |
| ロアーボールジョイントのハードポイントXYZ |
(3個の設計変数) |
| インナータイロッドとアウタータイロッドXYZ |
(6個の設計変数) |
| スピンドルのアラインメントポイントの位置XZ |
(2個の設計変数) |
- 結果
- この例では、この最適化方法がきわめて良好に機能します。
| 応答 |
ターゲット値 |
実際の値 |
| 設計位置のライドステア |
-4 °/m |
-4.107 °/m |
| フルジャウンス位置のライドステア |
-4 °/m |
-3.898 °/m |
| 設計位置のライドキャンバー |
+5 °/m |
+4.937 °/m |
| フルジャウンス位置のライドキャンバー |
+5 °/m |
+5.024 °/m |
| 設計位置のライドキャスター |
-8 °/m |
-8.402 °/m |
| フルジャウンス位置のライドキャスター |
-8 °/m |
-7.594 °/m |
例2
これはバス用とした別のサスペンションの例です。ここで実行するタスクは、必須の基準に合致するようにステアリングシステムを設計することです。適切な設計のステアリングシステムは以下のとおりです:
- ステアリングホイール角がゼロの場合、左右のホイールのステアもゼロになります。
- 最大ステアおよび最小ステアでは、左右のホイールのステアリング角の差異がゼロになる必要があります。
- ステアリング比とは、ステアリングホイールの回転数とホイールの回転数の比率を指します。ステアリングホイール角がゼロの状態のステアリング比は9.27になる必要があります。
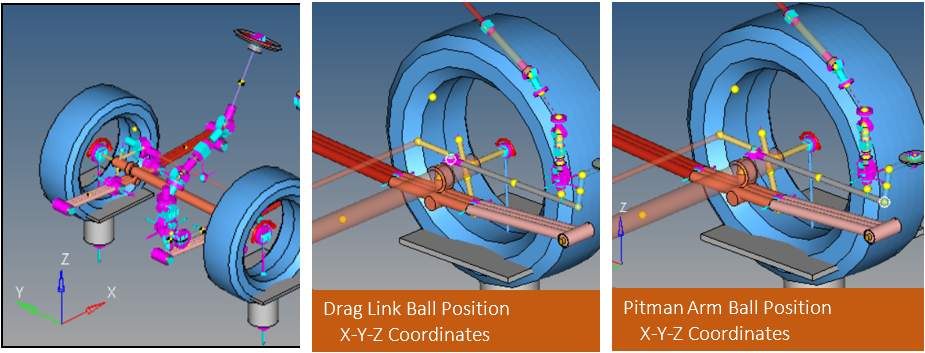
図 2.
この問題には次の4つの目的があります:
- ステアリングホイール角がゼロの状態の左ホイールのステア角 = 0
- ステアリングホイール角がゼロの状態の右ホイールのステア角 = 0
- 左右のホイールのステアリング角の差 = 0
- ステアリングホイール角がゼロの状態のステアリング比 = 9.27
- 設計変数
-
- ドラッグリンクボール位置のX-Y-Z座標
- ピットマンアームボール位置のX-Y-Z座標
- 結果
- この例では、この最適化方法がきわめて良好に機能します。取得される結果を以下に示します:
| 応答 |
ターゲット値 |
実際の値 |
| SWAゼロの左ステア |
0° |
+0.001° |
| SWAゼロの右ステア |
0° |
+0.000° |
| ステアリングの差(左対右) |
0° |
-0.003° |
| SWAゼロのステアリング比 |
9.27 |
9.271 |

