RMS2
測定した信号とターゲット曲線の間の、二乗平均平方根による面積差を計算します。
例
平面の4バー機構を設計するとします。この場合、カプラーリンクのCMのX座標と目標のプロファイルとの偏差を正確に表すメトリックが必要になります。RMS2応答によって、この必要な偏差メトリックが得られます。
カプラーリンクのCMのX座標で目標とするプロファイルは次のとおりです:
[(0.0, 199.997),
(0.1, 78.0588),
(0.2, -35.233),
(0.3, -102.140),
(0.4, -112.560),
(0.5, -78.718),
(0.6, -23.994),
(0.7, 36.862),
(0.8, 157.392),
(0.9, 260.213),
(1.0, 199.997)]
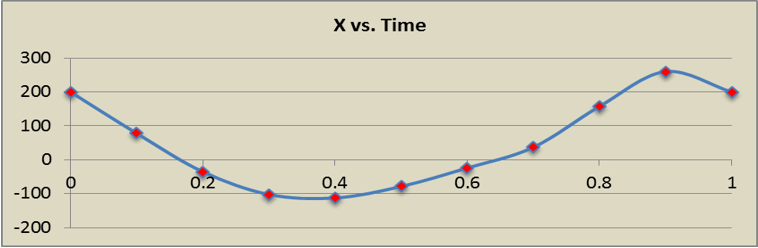
図 1.
以下のコードは、カプラーリンクのCMのX座標が示すRMS2応答を計算します。
>>> # Define the X vs. Time profile
>>> xy = [(0.0, 199.997),
(0.1, 78.0588),
(0.2, -35.233),
(0.3, -102.140),
(0.4, -112.560),
(0.5, -78.718),
(0.6, -23.994),
(0.7, 36.862),
(0.8, 157.392),
(0.9, 260.213),
(1.0, 199.997)]
>>>
>>> # Define the signal to be measured
>>> dx_coupler = "DX ({})".format(coupler.cm.id)
>>>
>>> # Define the RMS2 response
>>> rms2x = RMS2 (label = "Coupler-DX", targetValue = xy, measuredValue = dx_coupler)
この例のRMS2の計算は次のようになります。
X = (0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0)
Y = (199.997, 78.058, -35.233, -102.140, -112.560, -78.718, -23.994, 36.862, 157.392, 260.213, 199.997)
Spline = Spline (x=x, y=y)
Response =
X = (0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0)
Y = (199.997, 78.058, -35.233, -102.140, -112.560, -78.718, -23.994,
36.862, 157.392, 260.213, 199.997)
Spline = Spline (x=x, y=y)
Response =