Reference: PlantState

Model ElementReference_PlantStateは、作用点の周りのモデルの線形表現の生成に使用されるユーザー定義の状態のリストを定義します。線形表現は、固有値解析と状態マトリクス生成の両方で使用されます。

フォーマット

<Reference_PlantState 
     id= "integer" 
    [label= "string"] 
     num_element= "integer" 
     variable_id_list= "integer, integer, ..., integer" 
/>

属性

id: 要素識別番号を指定します。この番号は、すべてのReference_PlantState要素の中で一意です。; id > 0
label: Reference_PlantState要素の名前を示すオプション文字列。この説明は、主に、入力を読みやすくするために使用します。
num_element: このReference_PlantState要素で指定される状態の数。; num_element > 0
variable_id_list: 線形解析で使用する状態を定義する変数のIDを指定します。リストで指定する変数IDの数は、num_elementと正確に一致する必要があります。

多くのシステム、特に、回転システムの固有値と固有ベクトルは、運動方程式を線形化するために選択された状態に依存します。多くの場合、望ましい状態のセット（通常は実験的に測定されたものに相当する）が線形化に適しています。PSTATEは、このような状態を指定するために使用できるメソッドの1つです。
測定されたものに相当する状態とは異なる状態のセットを使用すると、誤った結果は生成されません。MotionSolveの結果は正しいですが、期待されるものではありません。

固有値と固有ベクトルが、システムの線形化に使用される状態に依存する物理システムの例をご参照ください。
状態マトリクス[A]、[B]、および[C]も、線形化されたマルチボディシステムを表現するために使用される状態に依存します。これを理解するために、状態x、入力u、および出力yの状態マトリクスのセットを考えます。このようなシステムの状態空間表現は次のとおりです：

$\begin{array}{l} \dot{x} = A x + B y \\ y = C x + D y \end{array}$

新しい状態のセット $z = H^{- 1} x$ が選択された場合、状態zを持つ状態空間方程式は次のようになります：

$\begin{array}{l} \dot{z} = \hat{A} x + \hat{B} y \\ y = \hat{C} x + \hat{D} y \end{array}$ 、ここで、 $\hat{A} = H A H^{- 1}, \hat{B} = H^{- 1} B, \hat{C} = C H, and \hat{D} = D$

作用点におけるシステム状態マトリクスの計算にユーザー定義の状態が使用される物理システムの例をご参照ください。
variable_id_listとnum_elementで指定される状態の数は、システムの自由度の数（N_DOF）以上にすることも以下にすることもできます。次の3つの可能性が存在します：
1. num_element < N_DOF
  この場合、MotionSolveは、線形方程式の定式化で、Reference_PlantStateで指定されたすべての状態を使用します。線形問題はN_DOF個の状態に関して定義する必要があるため、線形問題の定式化に必要な追加のN_DOF - num_element個の状態がMotionSolveによって自動的に選択されます。
2. num_element = N_DOF
  この場合、MotionSolveは、線形方程式の定式化で、Reference_PlantStateで指定されたすべての状態を使用します。すべての自由度が指定されるため、MotionSolveはこれらの状態のみを使用して線形問題を定式化します。
3. num_element > N_DOF
  この場合、MotionSolveは、線形方程式の定式化で、Reference_PlantStateで指定されたN_DOF個の状態のみを使用します。指定した状態の数が多すぎると、MotionSolveは警告を発します。余分なnum_element - N_DOF個の状態は破棄されて問題が解かれます。

PSTATEのvariable_id_listで変数を定義する式は、変位または角度の関数のみが可能です。

PSTATEの有効な定義を以下に示します：

<Reference_Variable  id = "71" type = "EXPRESSION" expr = "DM(11,12)"              /> 
<Reference_Variable  id = "72" type = "EXPRESSION" expr = "DX(22,33,44)"           /> 
<Reference_Variable  id = "73" type = "EXPRESSION" expr = "AZ(55,66)"              />
<Reference_PlantState    id = "7", num_element = "3"   variable_id_list = “71, 72, 73” />

PSTATEの無効な定義を以下に示します：変数82は速度の関数で、変数83は加速度の関数です。

<Reference_Variable  id = "81" type = "EXPRESSION" expr = "DM(11,12)"              /> 
<Reference_Variable  id = "82" type = "EXPRESSION" expr = "VX(22,33,44)"           /> 
<Reference_Variable  id = "83" type = "EXPRESSION" expr = "ACCZ(55,66)"            />
<Reference_PlantState    id = "8", num_element = "3"   variable_id_list = “81, 82, 83” />

MotionSolveは、無効なPSTATE定義にエラーとしてフラグを設定し、実行を停止します。

PSTATEのvariable_id_listで変数を定義する式は、線形独立である必要があります。PSTATEの以下の定義を考えます：
```
<Reference_Variable   id = "91"  type = "EXPRESSION"  expr = "Dx(71,62)"           /> 
<Reference_Variable   id = "92"  type = "EXPRESSION"  expr = "2* Dx(71,62)"        /> 
<Reference_PlantState id = "9",  num_element = "2"    variable_id_list = “91, 92”  />
```
VARIABLE id=92がVARIABLE id=91に対して線形従属であることは簡単に確認できます。実際、必ずVARIABLE id=91の値の2倍になっています。一方がわかれば、この関係を利用してもう一方の値を計算できます。2つ目のVARIABLEは、何ら新しい情報を提供しません。

このような場合、MotionSolveは、ユーザー定義の状態のいずれかが他の状態に対して線形従属であることを警告します。MotionSolveはその従属状態を無視します。線形化に使用するために必要であれば、代わりに内部状態を選択します。

例

下の図は、全体座標系のZ軸の周りを回転するヘリコプターブレードアセンブリの単純な表現を示しています。この例では、重力の影響は無視されます。

半径eの青色の円盤として示されたヘリコプターローターのハブは、その中心Oの周りを、全体座標系のZ軸について反時計回りに角速度ωで回転します。
オレンジ色で示されたヘリコプターブレードBは回転ジョイントでハブに取り付けられています。ブレードは、長さが2L、質量がm、その質量中心B*での全体座標系のZ軸周りの慣性モーメントがIです。

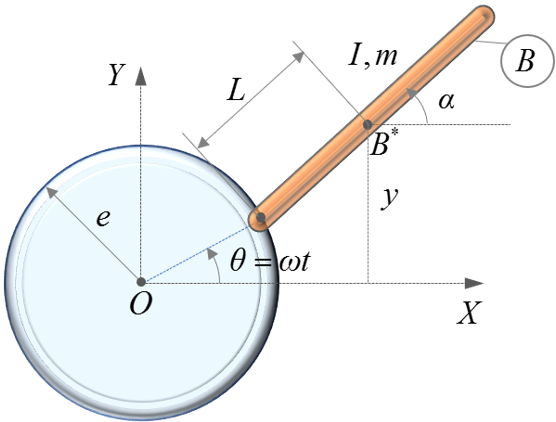
図 1.

このシステムの自由度は1です。運動方程式を定式化するには：

状態として、全体座標系X軸に対するブレードの角度αを選択します。
または、状態として、ポイントB*の全体座標系のy座標yを選択することもできます。

以下は、全く同じ計算を使用しても、同じ物理システムの2つの等価な非線形表現について、どの作用点における固有値も同じにはならないことを示しています。

状態 α	状態 y
運動方程式 $(I + m L^{2}) \ddot{α} + m e L ω^{2} \sin (α - ω t) = 0$
作用点 $t = 0, α =0, \dot{α} = ω$	作用点 $t = 0, y = 0, \dot{y} = (e + L) ω$
[A]マトリクス $A = [\begin{matrix} 0 & - \frac{m e L ω^{2}}{I + m L^{2}} \\ 1 & 0 \end{matrix}]$	[A]マトリクス $A = [\begin{matrix} 0 & - \frac{m e L ω^{2}}{I + m L^{2}} - ω^{2} \\ 1 & 0 \end{matrix}]$
以下の固有値： $m = 3, e = 2, I = 10, L = 10, ω = 10$ $λ_{1, 2} = \pm i \sqrt{\frac{m e L}{1 + m L^{2}}} ω = \pm 4.3994 i$	以下の固有値： $m = 3, e = 2, I = 10, L = 10, ω = 10$ $λ_{1, 2} = \pm i \sqrt{\frac{m e L}{1 + m L^{2}} + 1} ω = \pm 10.92496 i$

MARKER 34をB*に配置します。そのx軸はブレードの長さ方向に沿っており、そのz軸は全体座標系のz軸に沿っています。

MotionSolveに、線形化用の状態としてαを使用するように強制するには：

VARIABLEでαを定義します：

<Reference_Variable id = "22"  type = "EXPRESSION"  expr = "AZ(34)"            />

MotionSolveに、αを使用して線形化方程式を生成するように指示します：
```
<Reference_PlantState id = “3010”  num_element = “1”    variable_id_LIST = “22”/>
```

MotionSolveの固有値解析の結果は次のとおりです：

NUMBER   NATURAL_FREQ(HZ)  DAMPING_RATIO     REAL(HZ)          IMAG_FREQ(HZ)
     1   7.001886E-01      0.000000E+00      0.000000E+00      7.001886E-01
     1   7.001886E-01      0.000000E+00      0.000000E+00     -7.001886E-01

注: 7.001886E-01 HZ = 4.39941472 rad/s

MotionSolveの状態マトリクス解析の結果は次のとおりです：

A = [0.00000000000000000E+00, 1.00000000000000000E+00;
    -1.93548505949367993E+01,-1.91975649453440089E-06]

MotionSolveに、線形化用の状態としてyを使用するように強制するには：

VARIABLEでyを定義します：

<Reference_Variable id = "22"  type = "EXPRESSION"  expr = "DY(34)"            />

MotionSolveに、yを使用して線形化方程式を生成するように指示します：

<Reference_PlantState id = “3010”  num_element = “1”    variable_id_LIST = “22”    />

MotionSolveの固有値解析の結果は次のとおりです：

NUMBER   NATURAL_FREQ(HZ)  DAMPING_RATIO     REAL(HZ)          IMAG_FREQ(HZ)
     1   1.738762E+00      0.000000E+00      0.000000E+00      1.738762E+00
     1   1.738762E+00      0.000000E+00      0.000000E+00     -1.738762E+00

MotionSolveの状態マトリクス解析の結果は次のとおりです：

A = [0.00000000000000000E+00, 1.00000000000000000E+00;
    -1.19354838709666097E+02, 1.71456230219270937E-13]

注: 1.738762E+00 HZ = 10.9249639 rad/s

Reference: PlantState

フォーマット

属性

コメント

例