MV-9001:シンプルな振子のチュートリアル
本チュートリアルでは、Msolve MotionSolve Python APIを用いてシンプルな自由度1の機構をモデル化する方法を学びます。
本チュートリアルをIPython notebookとして実施している場合、SHIFT-ENTERをクリックすることにより、各コードセルを内部的に実行することが可能です。Pythonコードの出力(存在する場合)が表示され、実行すると次のセルにジャンプします。

図 1.
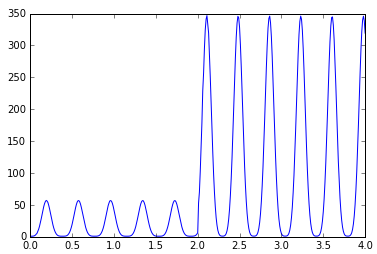
剛体は質量0のワイヤーで吊り下げられており、ヒンジジョイントを介して地面に接続されています。システムに作用する唯一の力は、負の垂直方向に沿って指示された重力です。シミュレーションでは、初期の静止位置からパートが揺れる様子を示しています。ジョイントには摩擦力がなく、また、その部分に作用するエネルギー散逸力のいずれのタイプもないため、ボールはフルスイングごとに180度の角変位に達します。
ジョイントの反力を調べます。
msolveモジュールの読み込み
In [1]: from msolve import*上記のコマンドを実行するには、msolveモジュールがコンピュータのパスになければなりません。上記が成功したと仮定すると、msolveの名称は現在のネームスペースにインポートされています。これにより、msolveで定義されているすべてのクラスと関数にアクセスできるようになり、シンプルな振子の作成を開始することができます。
モデルの作成
振子の機構を作成するにはまず、モデルを作成する必要があります。モデルは、すべてのエンティティの親として機能するコンテナに他なりません。モデルクラスは、MotionSolveの出力ファイル名を指定するためのキーワード引数を取ります。名称pendulumを使用することが可能です。
In [2]: model = Model(output='pendulum') 単位と重力の追加
モデルを作成した後、単位、重力や地面などのエンティティを追加することができます。ほとんどのエンティティはデフォルトのプロパティを有しています。たとえば、引数を指定せずにソルバーの単位セットを作成する場合、基本的にはSI単位を作成していることになります。
msolveのクラス名ではCapWordsの規約を使用し、Pythonのヘルプシステムを使用して各msolveクラス、その使用方法、プロパティについて学ぶことができます。例として以下の手順を実行してください。
ポイントの定義
MBSの中には、ポイントを使って定義されているモデルもあります。ポイントは、x、y、zの位置と便利な手法を擁する特別な補助オブジェクトです。これらはメカニズムを定義する強力な方法であり、モデル内でX、Y、Z量が必要な場所であればどこでも使用できます(例えば、パーツの位置決めやマーカーの原点の位置決めなど)。
この例では、ポイントを使用して、3次元空間内の様々なオブジェクト(マーカーなど)の位置を特定します。マーカーの位置や向きを定義するときにポイントを使用できます。
In [8]: p0=Point() マーカーの作成
このポイントを利用して、地面マーカーの原点を特定することができます。マーカーは、空間内の幾何学的なポイントと、その点から出ている互いに直交する3つの座標軸のセットによって定義されます。
マーカークラスでは、プロパティqpは、ボディ参照フレーム内のマーカー原点の位置に対応します。ボディとして地面を使用しているため、qpは全体参照フレーム内のマーカーの位置です。zp, xpメソッドを使用して、Z軸とX軸を方向付けします。
パート作成の検証
各エンティティは、インタラクティブに検証することが可能です。これは、正しいモデルだけがシミュレーションされるようにするための方法です。上のコードセルで作成したパートには質量プロパティがありますが、重心マーカーを有しません。したがって、これは正しくありません。以下を行うことができます:
形状オブジェクトの作成
アニメーションのために、形状オブジェクト、ここでは球体を作成することができます。ドキュメントによると、球体には重心マーカーとその半径が必要とされます。
In [13]: sphere=Sphere (cm=part.cm, radius=20) ジョイントとリクエストの追加
球体は、適切に拘束する必要があります。そうしないと落下します。振子は、ヒンジ点p0の回転ジョイントを使用してモデル化することができます。これにより、振子ボディの変形不可能で地面への剛性無限大かつ質量0の接続を効果的に捉えることが可能です。回転ジョイントは、振子の球体上と地面上の2つのマーカーを接続し、これらのマーカーを3次元空間内に適切に配置する必要があります。
回転ジョイントの要件は、iとjのマーカーが一致していることと、そのZ軸が適切に配置されていることです。
リクエストも作成します。リクエストはMotionSolveの出力チャンネルを定義し、MotionSolveの出力ファイルに書き込まれ、HyperGraphによるプロッティングや信号処理に使用されます。リクエストは、ランタイム式、組み込み関数(MOTION、FORCE、FIELDなど)、またはユーザーが作成した関数を使用して定義することができます。
この場合、定義済みの"FORCE"メソッドを使用して力のリクエストを作成し、MotionSolveランタイム関数AXを使用して角変位を追跡する別のリクエストを作成することができます。AXは、2つのマーカー間の角変位をラジアン単位で測定します。
シミュレーションの実行
この時点で、過渡解析を実行する準備が整っています。シミュレート手法はMBSモデル上で呼び出されます。モデルを構成する各エンティティに、検証プロセスが実行されます。これは、正しいモデルのみがシミュレートされていることを確認するために必要なステップです。シミュレートコマンドは、オプションのフラグreturnResultsをTrueに設定して呼び出すことができます。これは以下のコードで示すように、シミュレーションの結果をさらにポスト処理を行うために実行コンテナに保存します。