Constraint: Joint

Model ElementConstraint_Jointを使用して、2つのボディ間の理想化されたコネクターを指定します。

説明

Constraint_Jointは、低次対偶拘束のセットを定義します。物理的に、このジョイントは、特定の方向のみの相対的並進および / または回転運動が可能な2つのあわせ面から成ります。これらの面は取り去られ、その関係性は常に、2つのボディ上のポイントと方向間の方程式のセットとして表されます。

フォーマット

<Constraint_Joint
     id             =     "integer"     
     label          =     "Name of Joint"
     type           =     "CONSTANT_VELOCITY"
                          "CYLINDRICAL"
                          "FIXED"
                          "FREE"
                          "HOOKE"
                          "INLINE"
                          "INPLANE"
                          "ORIENTATION"
                          "PARALLEL_AXES"
                          "PERPENDICULAR"
                          "PLANAR"
                          "RACK_PINION"
                          "REVOLUTE"
                          "SCREW"
                          "SPHERICAL"
                          "TRANSLATIONAL"
                          "UNIVERSAL"
     i_marker_id     =    "integer"     
     j_marker_id     =    "integer"   
   [ pitch           =    "real" ]   
   [ pitch_diameter  =    "real" ]
   [ is_virtual      =   {"FALSE" | "TRUE"} ]
/>

属性

id

要素識別番号（整数 > 0）。これは、すべてのConstraint_Joint要素の中で一意の番号です。

label

Constraint_Joint要素の名前。

i_marker_id

1つ目のボディ上の結合を定義するReference_Markerを指定します。ボディは、剛体、弾性体、またはポイントボディのいずれかです。このパラメータは必須です。

j_marker_id

1つ目のボディ上の結合を定義するReference_Markerを指定します。ボディは、剛体、弾性体、またはポイントボディのいずれかです。

type

i_markerとj_marker_idの間の拘束結合のタイプを指定します。

は、次のいずれかにできます：

"CONSTANT_VELOCITY"

"CYLINDRICAL"

"FIXED"

"FREE"

"HOOKE"

"INLINE"

"INPLANE"

"ORIENTATION"

"PARALLEL_AXES"

"PERPENDICULAR"

"PLANAR"

"RACK_PINION"

"REVOLUTE"

"SCREW"

"SPHERICAL"

"TRANSLATIONAL"

"UNIVERSAL"

このパラメータは必須です。これらのジョイントタイプの詳細については、コメント5-21をご参照ください。

pitch

スクリュージョイントのピッチを定義します。このピッチによって、このスクリュージョイント内の並進運動と回転運動の比が決まります。

このパラメータは、TYPE = "SCREW_JOINT"の場合にのみ必要となります。

pitch_diameter

ラックアンドピニオンギアの拘束におけるピニオンギアのピッチ円直径を定義します。

このパラメータは、TYPE= "RACK_PINION"の場合に必須です。

is_virtual

仮想拘束なのか通常の拘束なのかを定義します。is_virtualがTRUEに設定されている場合、拘束は仮想拘束として実装されます。is_virtualがFALSEに設定されている場合、拘束は通常の代数拘束として実装されます。このパラメータは省略可能です。デフォルトはFALSEです。仮想ジョイントの詳細については、コメント22をご参照ください。

例

次の図は、単振り子システムを示しています。このシステムは、ポイントPにおいて地面Gに固定されている剛体バーBからなります。バーBの質量中心は、Reference_Marker B*で示されています。

Pにおける結合では、B上とG上の対応する材料ポイント（それぞれP₁とP₂）が常に重ねられる必要があります。さらにこの結合では、P₁で紙の平面から突き出ている軸と、P₂に位置する2つ目の軸が、常に同一線上にある必要があります。これは"REVOLUTE"タイプの結合です。

重力は全体座標系のYの負方向に作用しています。重力の影響によって、全体座標系のX-Y平面内でバーBが揺れますが、P1とP2は重なり合ったままであり、2つの軸は同一線上のままであるという要件は満たしています。

図 1. REVOLUTEジョイントの使用例を示す単振り子システム

以下のオブジェクトを入力データファイル内で定義するとします：

P₁ = 地面上のReference_Marker 11、平面から突き出ているz軸
P₂ = ボディB上のReference_Marker 21、平面から突き出ているz軸

Constraint_Jointオブジェクトは次のように定義できます：

<Constraint_Joint
     id           = "1"
     label        = "Name of Joint"
     i_marker_id  = "21"
     j_marker_id  = "11"
     type         = "REVOLUTE"
/>

Constraint_Jointは、モデル内の一連の拘束条件を定義します。これらの拘束では、2つの結合されたボディは特定方向の相対運動のみが可能です。他のすべての方向の運動は禁止されます。このシステムは、それらの方向に動かないように“拘束”されます。
最も一般的な形では、拘束には変位、速度、および時間を含めることができます。Constraint_Joint要素の特徴は、変位のみが含まれるという点です。これらの拘束関係に、速度や時間は明示的に含まれません。したがって、これらの拘束関係によってシステムのエネルギーが追加されたり除去されたりすることはありません。
内部の反力や反モーメントは、Constraint_Joint内の各拘束に関連付けられています。この内部反作用によって、コネクター内で指定されたボディの相対運動が拘束を満たすことが保証されます。Constraint_Joint内の反力にアクセスするには、JOINT()関数式を使用します。
ジョイントの各Reference_Markerにおける内部の反力と反モーメントは、ニュートンの運動の第三法則に従います。これらは、互いに打ち消し合うような大きさと方向で作用します。
モデル内の拘束は“過剰指定”できます。この場合は、システムは過拘束されていると表現され、これらの拘束は“余剰”と呼ばれます。
次の図 2に示しているフレームに結合されたドアについて考えてみましょう。

図 2. 余剰に拘束されたシンプルなシステム

ドアとフレームはどちらも剛体と見なされます。3つのヒンジによってドアがフレームに結合されることで、ドアは開閉が可能となります。これらのヒンジは回転ジョイントとしてモデル化されます。この理想化では、ヒンジは無質量の剛体と見なされます。各ヒンジによって、図 2で赤い矢印で示された軸の周りでドアとフレームの間の回転が可能になります。
この理想化では、以下のことに留意する必要があります：
- これらのヒンジの軸は完全に同一線上にある必要があります。そうでない場合、ドアは開閉できません。
- 本当に必要なのは1つのヒンジのみです。他の2つは“余剰”です。
  このようなシステムが与えられると、MotionSolveは、過拘束を検知し、2つのヒンジに相当するものをモデルから除去して、正しいモーションが予測されるようにシステムを解析します。
  
  2つのヒンジが解析プロセスから除去されると、それらの反力はゼロに設定されます。明らかに、これは想定外の挙動です。現実には、3つのヒンジすべてが反力と反トルクを有しています。これは、システムの理想化に関する問題です。2つのボディ（ドアとフレーム）の少なくとも1つが弾性化されると、各ヒンジでより現実的な反作用が見られます。
TYPE = "CONSTANT_VELOCITY"
等速ジョイントは、非常に複雑なサブシステムです。これは、出力シャフトと入力シャフトの角速度が、その相対的な向きに関係なく等しくなるようにします。図 3に、等速ジョイントの構造を示します。

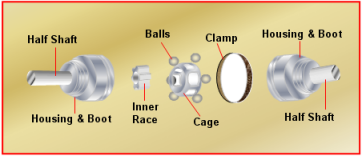
図 3. CONSTANT_VELOCITYジョイント

等速ジョイントの細部は取り除かれています。すなわち、すべての中間パートは無視され、シンプルな代数拘束のセットを通じて、これらのシャフト間の入出力関係が捕捉されます。エネルギー損失はモデル化されません。
TYPE = "CYLINDRICAL"
円筒ジョイントは、拘束されるボディ間に2自由度を与えます。図 4 は、円筒ジョイントの概略図を示しています。この円筒ジョイントによって、一方のボディ（Body-1）は、もう一方のボディ（Body-2）で定義された固定軸に沿って並進し、この軸の周りを回転することが可能になります。

図 4. CYLINDRICALジョイント
TYPE = "FIXED"
固定ジョイントは、2つのボディが溶接されているかのように一体的に動くように強制します。これらの2つのボディ間の相対運動はありません。図 5 は、固定ジョイントの概略図を示しています。

図 5. FIXEDジョイントの概略図

Body-2上に“刻印”された任意の座標系の位置と向きは、Body-1上に“刻印”された任意の座標系に対して固定されています。
TYPE = "FREE"
フリージョイントは、固定ジョイントの正反対です。これは、結合する2つのボディ間のどのようなモーションも制限しません。フリージョイントは主に、ジョイント座標（相対座標とも呼ばれます）を使用して内部的にシステムを表す場合に、トポロジー階層を定義するために使用されます。

図 6. FREEジョイント

フリージョイントでは、Body-2に固定された任意の座標系は、Body-1に固定された座標系に対して、あらゆる動きが可能です。
TYPE = "HOOKE"
次の図は、HOOKEジョイントの概略図を示しています。このジョイントは、Body-1上のIとBody-2上のJの2つのReference_Markerを、（a）それらの原点O_iとO_jが常に重なり合うように、（b）Iマーカーのx軸がJマーカーのy軸と常に直交するように、拘束します。

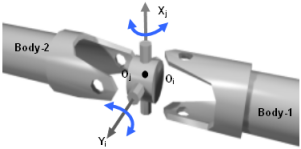
図 7. HOOKEジョイント

HOOKEジョイントは、システムから4つの自由度を除去します。Body-1はXi軸の周りを回転でき、Body-2はYi軸の周りを回転できます。相対的な並進はできません。物理的には、HOOKEジョイントはUNIVERSALジョイントとまったく同じです。
TYPE = "INLINE"
これは、Body-1上のReference_Markerの原点が、Body-2に配置されたReference_Markerのz軸に沿って並進することを要求する拘束プリミティブです。すべての回転が可能です。図 8 は、INLINEプリミティブの概略図を示しています。

図 8. INLINEジョイントの概略図

このインラインプリミティブは、2つの並進自由度を拘束します。これによって、Body-2上のReference_Markerのx軸とy軸に沿った並進が妨げられます。
TYPE = "INPLANE"
これは、Body-1上のReference_Marker（下図のI）の原点が、J Reference_Markerの原点とz軸によって定義されるXY平面内に留まるようにすることを要求する拘束プリミティブです。図 9 は、INPLANEプリミティブの概略図を示しています。

図 9. INPLANEジョイントの概略図

INPLANEプリミティブは、1つの並進自由度を拘束します。これによって、Body-2上のReference_Marker Jのz軸に沿った並進が妨げられます。すべての回転が可能です。
TYPE = "ORIENTATION"
図 10 は、ORIENTATIONジョイントの概略図を示しています。これは、Body-1上のReference_Marker（下図のI）の向きが、Body-2上のReference_Marker（下図のJ）の向きと常に同じになるようにすることを要求します。

図 10. ORIENTATIONジョイント

ORIENTATIONジョイントは、3つの自由度（すべて回転自由度）を除去します。Body-2に対するBody-1の3つすべての並進が可能です。
TYPE = "PARALLEL_AXES"
図 11 は、PARALLEL_AXESジョイントの概略図を示しています。このジョイントは、Reference_Marker（下図のI）のz軸が、Body-2上のReference_Marker（下図のJ）のz軸に常に平行になるように、Body-1を拘束します。

図 11. PARALLEL_AXESジョイント

PARALLEL_AXISジョイントは、2つの回転自由度を除去します。Body-1の回転は、I Reference_Markerのz軸の周りについてのみ可能です。並進については3つすべて可能です。
TYPE = "PERPENDICULAR"
図 12 は、PERPENDICULAR_AXESジョイントの概略図を示しています。このジョイントは、Reference_Marker（下図のI）のz軸が、Body-2上のReference_Marker（下図のJ）のz軸に常にPERPENDICULARになるように、Body-1を拘束します。

図 12. PERPENDICULAR_AXESジョイント

PERPENDICULAR _AXISジョイントは、1つの自由度を除去します。Body-1の回転は、I Reference_Markerのz軸の周りとJ Reference_Markerのz軸の周りについてのみ可能です。並進については3つすべて可能です。
TYPE = "PLANAR"
平面ジョイントは、Body-1上で定義されたReference_Marker Iの動きを制限することで、その原点が常に、BODY-2上で定義されたReference_Marker Jの原点によって定義されたx-y平面内に含まれるようにすることを要求します。図 13 は、PLANARジョイントの概略図を示しています。

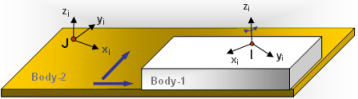
図 13. PLANARジョイントの概略図

PLANARジョイントは、平面内の2つの並進自由度と、1つの“面内”回転自由度の3つの自由度を与えます。
TYPE = "RACK_PINION"
図 14 は、ラックアンドピニオンジョイントを示しています。ピニオンギアPは、紙の平面から突き出る軸の周りの回転が可能となるようにハウジング（非表示）に結合されています。ラックRは、左から右にスライドします。RACK_PINIONジョイントは、ピニオンの回転θ_pをラックの並進Sに対応付けます。

図 14. RACK_PINIONジョイント

RACK_PINIONジョイントは、5つの自由度を与えます。これは、1つの拘束のみをシステムに適用します。
TYPE = "REVOLUTE"
図 15 は、REVOLUTEジョイントの概略図を示しています。このジョイントは、2つのReference_Marker、IとJを、（a）それらの原点が常に重なり合うように、（b）これらのz軸が常に同一線上にあるように、拘束します。

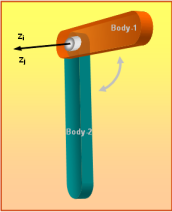
図 15. REVOLUTEジョイント

REVOLUTEジョイントは、システムから5つの自由度を除去します。可能なモーションは、共通のz軸周りの回転のみです。
TYPE = "SCREW"
図 16 は、スクリュージョイントを示しています。Body-2には、ピッチpのねじ山が設けられています。スクリューの軸は、Body-2上のReference_Marker Jのz軸によって定義されます。Body-1には、Body-2のねじ山とかみ合うように対応するねじ山が設けられています。スクリュー軸周りにBody-2が回転すると、Body-1はスクリュー軸に沿って上下に並進します。SCREWジョイントは、スクリュー軸周りのBody-1の回転をスクリュー軸に沿った並進に関連付けます。

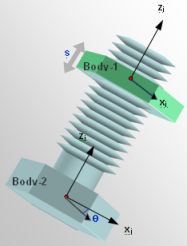
図 16. SCREWジョイント

SCREWジョイントは、システムから1つの自由度のみを除去します。
TYPE = "SPHERICAL"
SPHERICALジョイントは、SPHERICALジョイントの概略図を示しています。このジョイントは、Body-1上のIとBody-2上のJの2つのReference_Markerを、これらの原点O_iとO_jが常に重なり合うように拘束します。

図 17. SPHERICALジョイント

SPHERICALジョイントは、システムから3つの自由度を除去します。Body-2は、Body-1に対して回転できます。相対的な並進はできません。
TYPE = "TRANSLATIONAL"
図 18 は、TRANSLATIONALジョイントの概略図を示しています。このジョイントは、IとJの2つのReference_Markerを、（a）これらの向きが同じままになるように、（b）これらが単一の並進軸（Reference_Marker Jのz軸）を共有するように、拘束します。

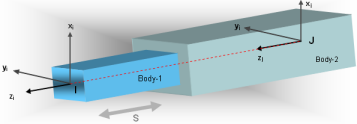
図 18. TRANSLATIONALジョイント

TRANSLATIONALジョイントは、システムから5つの自由度を除去します。可能なモーションは、Reference_Marker Jのz軸に沿った相対並進のみです。
TYPE = "UNIVERSAL"
図 19 は、UNIVERSALジョイントの概略図を示しています。このジョイントは、Body-1上のIとBody-2上のJの2つのReference_Markerを、（a）これらの原点O_iとO_jが常に重なり合うように、（b）これらのz軸が常に直交するように、拘束します。

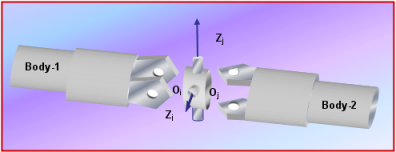
図 19. UNIVERSALジョイント

UNIVERSALジョイントは、システムから4つの自由度を除去します。Body-2はZ_j軸の周りを回転でき、Body-1はZ_i軸の周りを回転できます。相対的な並進はできません。

出力角速度は、入力角速度と等しくならないことに留意してください。
次のように仮定すると：
- ù：入力シャフトの速度
- ù2：出力シャフトの速度
- â：両シャフト間の角度
- f1：入力シャフトの回転角度
  次の式が成り立ちます：(1)
  $ω_{2} = \frac{ω_{1} \cos β}{1 - \sin^{2} β \sin^{2} ϕ_{1}}$
β=π/2では、出力角速度はゼロです。物理的には、両方のシャフトはしっかりと組み合わさっています。このことは、MotionSolveで非正則マトリクスとして表現されます。

β=0においてのみ、出力シャフトの角速度が入力シャフトの角速度と等しくなります。

出力シャフトの角加速度α2は、次のように表現できます：(2)
$α_{2} = \frac{ω_{1}^{2} \sin^{2} β \cos β \sin 2 ϕ_{1}}{{(1 - \sin^{2} β \sin^{2} ϕ_{1})}^{2}}$
マルチボディダイナミクスでは、通常のジョイントや理想的なジョイントは、次のように一連の代数拘束方程式として定義できます：
$Φ (q) = 0$

ここでqは、システムの一般化座標です（各剛体の位置と向きなど）。この一連の拘束方程式が、Lagrangeの未定乗数法を使用してMotionSolveで運動方程式（EOM）に組み込まれることで、一連の微分代数方程式（DAE）が形成されます。それぞれの拘束方程式は、マルチボディシステムの自由度（DOF： degree of freedom）を1だけ減少させます。この機構の合計運動DOF数は、一般化座標qの数から、マルチボディシステムの代数拘束方程式の数を引いた数です。このジョイントを仮想化した場合は、拘束方程式は次のように拡張されます：

$ε - Φ (q) = 0$

ここでεは、追加の一般化座標として扱われ、DAEの他の一般化座標qと共に解かれます。EOMと共に代数方程式を解く代わりに、εを最小化するために、制約違反と反対方向に作用する違反力を導入することもできます。この力は次のように定義されます：

$f = - G (\ddot{ε} + 2 \sqrt{K} \dot{ε} + K ε)$

ここで、Gは非常に大きい係数であり（通常は1e12程度）、Kは任意の剛性です（K = 1など）。この方程式は、2次システム（質量スプリングダンパなど）とよく似ており、臨界減衰を示す減衰係数が選択されます。GとKの正確な値はソルバーに固有であり、システムの全体的な特性に基づいて自動的に調整され、手動で変更することはできません。その後、力fが運動方程式のRHSに追加されます。

この巨大要素の手法と一般的なペナルティ手法（ブッシュを参照）の違いは、違反またはペナルティの程度にあります。この新しい手法では、εはごく小さな値に保たれるため、多くのケースでは、ソルバーで大きい負荷（数値的剛性）を生成することなく拘束違反を検知することはできません。ユーザーの観点からは、通常および仮想のジョイント / 拘束は、同じ運動特性と物理特性をもたらしますが、唯一の相違点として、仮想のジョイント / 拘束は過拘束を生じさせることはできません。さらに、仮想のジョイント / 拘束は、他の数値的手法で一般運動方程式を解くことを可能にする“ソフト結合”と考えることができます。

仮想拘束は、すべての解析タイプで使用できます（静解析、擬似静解析、過渡解析、線形解析など）。仮想拘束は、代数拘束として、解析内でアクティブ化したり非アクティブ化したりできます。