Control: SISO
Model ElementControl_SISOは、ラプラス領域内で線形かつ時不変の動的システムを定義する抽象モデリング要素です。SISOは、Single Input Single Output(単入力単出力)を意味します。
説明
このような動的システムは伝達関数によって表されます。実際、伝達関数は多くの場合、曲線のフィッティングの前に行われる実験によって特性が示されます。この要素のモデリング用途としては、アクチュエーター(電動、油圧、空気圧)、振動絶縁装置(ブッシュとショックアブソーバー)、コントローラー(PID)が挙げられます。
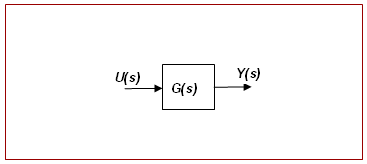
図 1. Control_SISO要素のブロック図表現
m とnは、分子多項式と分母多項式の次数を表し、m ≤ nを満たしている必要があります。

図 2. 動的システムの入力、出力および状態
フォーマット
<Control_SISO
id = "integer"
[ label = "string" ]
x_array_id = "integer"
y_array_id = "integer"
u_array_id = "integer"
[ is_static_hold = { "TRUE" | "FALSE" } ]
num_numerator_coef = "integer"
numerator_coef = "real [ real real … real ] "
num_denominator_coef = "integer"
denominator_coef = "real [ real real … real ] "
/>属性
- id
- 要素識別番号(整数 > 0)。この番号は、すべてのControl_SISO要素の中で一意です。
- label
- Control_SISO要素の名前。
- x_array_id
- このControl_SISOの状態xを格納するために使用するReference_ArrayのIDを指定します。このIDを持つARYVAL()関数を使用することで、MotionSolveの式のこの状態にアクセスすることができます。また、SYSFNCおよびSYSARYでこのIDを使用することで、ユーザーサブルーチンの状態値にアクセスすることもできます。
- y_array_id
- このControl_SISOの出力yを格納するために使用するReference_ArrayのIDを指定します。このIDを持つARYVAL()関数を使用することで、MotionSolveの式のこの状態にアクセスすることができます。また、SYSFNCおよびSYSARYでこのIDを使用することで、ユーザーサブルーチンの出力値にアクセスすることもできます。
- u_array_id
- このControl_SISOの入力uを格納するために使用するReference_ArrayのIDを指定します。このIDを持つARYVAL()関数を使用することで、MotionSolveの式のこの状態にアクセスすることができます。また、SYSFNCおよびSYSARYでこのIDを使用することで、ユーザーサブルーチンの入力値にアクセスすることができます。
- is_static_hold
- 要素識別番号(整数 > 0)。この番号は、すべてのControl_SISO要素の中で一意です。
- num_numerator_coef
- Control_SISOの分子に含まれる係数の数を指定する整数。num_state > 0。
- numerator_coef
- 伝達関数の分子多項式の係数を"s"の昇冪で指定します。
- num_denominator_coef
- Control_SISOの分母に含まれる係数の数を指定する整数。num_numerator_coef ≤ num_denominator_coef。
- denominator_coef
- 伝達関数の分母多項式の係数を"s"の昇冪で指定します。
例
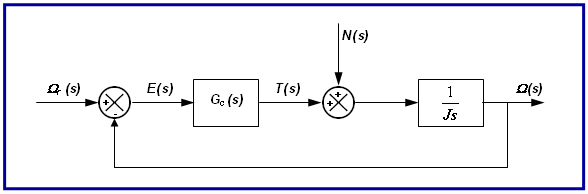
図 3. ローター速度制御システムのブロック図
- Ωr(s)は、基準速度を示します。
- Ω(s)は、実際の速度を示します。
- E(s)は、誤差信号のラプラス変換を示します。
- Gc(s)は、コントローラーの伝達関数を示します。
- T(s)は、コントローラーの出力である制御トルクを示します。
- Jは、ローターの慣性モーメントを示します。
- N(s)は、ラプラス領域内の外乱荷重を示します。
K とKpは、コントローラーの利得を示します。このコントローラーは、Control_SISOを使用して次のようにモデル化できます:
<Control_SISO
id = "303001"
label = "ControlSISO name"
x_array_id = "30300200"
y_solver_id = "30300300"
u_solver_id = "30300100"
is_static_hold = "FALSE"
num_numerator_coef = "2"
numerator_coef = "10. 1."
num_denominator_coef = "2"
denominator_coef = "0. 1."
/>
図 4. ローターの速度と時間の関係を表すプロット
コメント
- Control_SISOは、多くの分野にわたるシステムのモデル化において、さまざまな用途に適用できる多目的要素です。この要素を使用して、伝達関数によって表される外部で定義された任意のサブシステムをモデル化できます。MotionSolve内のシステムモデルに“統合”できるサブシステムの例としては、以下が挙げられます:
- PIDなどのコントローラー
- 油圧式 / 空気圧式 / 電気機械式のアクチュエーター
- 1次遅れ要素
- 人間の運転動作を再現するシンプルなドライバモデル
- 振動絶縁装置の周波数および振幅依存特性
- ラプラス領域の伝達関数を時間領域の状態空間形式に変換するアルゴリズムは、高次システムに対しては堅牢ではありません。このような場合は、まずこの伝達関数を低次の伝達関数に因数分解してから、因数ごとに1つのControl_SISO要素を使用することをお勧めします。
- 静解析時および擬似静解析時のControl_SISO要素に関連する動的状態の挙動は、属性is_static_holdによって制御されます。
is_static_hold = "TRUE"
時間T=0で解析が行われる場合、状態は、IC配列によって指定された値で固定されたままです。動解析の後に解析が行われる場合、値は動的シミュレーションから取得された最後の値で固定されたままです。Control_SISOの状態を定義する方程式は、以下に置き換えられます:
x(t*) = x*、ここでx*は定数です。
動的状態が固定されたままの場合、その時間導関数は、静的平衡または擬似静的ステップの最後でゼロにはならなくなります。入力値uは、この時点で変化しています。これにより、その後動解析が実行される場合、その解析で過渡応答が生じる可能性があります。
is_static_hold = "FALSE"
解析プロセスの間、状態は一定に保たれず、システム全体のコンフィギュレーションの変化に従って変えることができます。これがどのように実現されるかを以下に示します:
静解析および擬似静解析では、動的状態の導関数はゼロに設定されます。これにより、Control_SISOがこれら2つの解析の一連の代数方程式に変換されます。
微分方程式は次のようになります:
Ax+Bu=0
平衡解析では、システムのコンフィギュレーションが変化すると、平衡条件を満たすように入力uが変化します。上記の式が解かれ、現在のuの値に対するxが計算されます。
この方法により、静解析や擬似静解析の終了時に、動的状態の時間導関数が確実にゼロになり、後続の動解析が滑らかになります。