Force: Beam

説明

ビームの質量は、IマーカーとJマーカーの原点に集中しています。ビームの剛性プロパティは、ティモシェンコ梁理論を使用して求められます。ビームの軸は、J Reference_Markerのx軸に沿っているとします。また、J Reference_Markerのx軸は、非変形ビームの中立軸になるように定義されます。ビームは、わずかな回転振れが生じるものとします。大きな回転はサポートされません。

フォーマット

<Force_Beam
     id                  = "integer"   
   [ label               = "string" ]     
     i_marker_id         = "integer"     
     j_marker_id         = "integer"     
     length              = "real"     
     E                   = "real"     
     G                   = "real"     
     area                = "real"     
     ixx                 = "real"     
     iyy                 = "real"     
     izz                 = "real"     
     ASY                 = "real"     
     ASZ                 = "real"     
     cratio              = "real"     
     preload_x           = "real"     
     preload_y           = "real"     
     preload_z           = "real"     
     preload_tx          = "real"     
     preload_ty          = "real"     
     preload_tz          = "real"
</Force_Beam>

属性

id

要素識別番号（整数 > 0）。この番号は、Force_Beam要素の中で一意であり、要素を一意に特定します。

label

Force_Beam要素の名前。

i_marker_id

力が適用されるReference_Markerを指定します。これは力の作用点として指定されます。

j_marker_id

反力および反モーメントが適用されるReference_Markerを指定します。これは力の反作用点として指定されます。j_marker_idのx軸は、ビームの中立軸を定義します。y軸とz軸の向きは、断面の主軸に沿っている必要があります（断面相乗モーメントが0）。コメント2をご参照ください。

length

ビームの自由長を指定します。これは、j_marker_idの原点からi_marker_idの原点までの距離です。対応するベクトルは、j_marker_idのx軸に沿っている必要があります。下記のコメント2をご参照ください。

E

ビーム材料のヤング率を指定します。ビームは、その材料プロパティ内で均一であると見なされます。E > 0。

G

ビームの弾性率を指定します。これは、次の式によるヤング率とポアソン比に関係します：

G = E/2(1+v)、ここでvはポアソン比です。G > 0。

area

ビームの中立軸に垂直な断面の面積を指定します。これは、ビームの長さ方向に沿って一定であると想定されています。area > 0

ixx

断面のねじり剛性形状係数を指定します。

円形断面の場合、ixxは極慣性モーメントと一致します。非円形断面の場合、ねじり剛性定数は極慣性モーメントと一致しません。通常は、ねじりに関連するそりの影響により大幅に小さくなります。詳細については、コメント11をご参照ください。ixx > 0。

iyy

j_marker_idのy軸と平行な断面上の軸に関する、ビーム断面の断面2次モーメントを定義します。iyy > 0。

izz

j_marker_idのz軸と平行な断面上の軸に関する、ビーム断面の断面2次モーメントを定義します。izz > 0

ASY

ティモシェンコ梁のy方向のせん断面積比を指定します。この値では、Y方向のせん断たわみが考慮されます。これは次のように定義されています：

(1)

Q_y は、y方向の力によってせん断される断面の断面1次モーメントです。l_zは、z方向の断面寸法です。I_yyは、ビームのy軸に関する断面2次モーメントです。y方向のせん断変形を無視するには、ASY=0を設定します。詳細については、コメント14をご参照ください。ASY ≥ 0

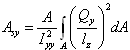
ASZ

ティモシェンコ梁のz方向のせん断面積比を指定します。この値では、Z方向のせん断たわみが考慮されます。これは次のように定義されています：

(2)

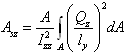
Q_z は、z方向の力によってせん断される断面の断面1次モーメントです。l_yは、y方向の断面寸法です。I_zzは、ビームのz軸に関する断面2次モーメントです。

z方向のせん断変形を無視するには、ASZ=0を設定します。詳細については、コメント14をご参照ください。ASZ > 0。

cratio

ビームの減衰比を定義します。ビーム減衰マトリクスは、ビーム剛性マトリクスにcratioを乗算することによって計算されます。言い換えると、次のようになります：

[C] = cratio * [K]

通常は、0.01（1%）の値がcratioに使用されます。

cratio≥ 0。

preload_x, preload_y, preload_z

ビームに対するプリロードとして適用されるX、Y、またはZ方向の力を定義します。シミュレーション時にX、Y、またはZ方向に沿って計算された力に加えて、指定されたプリロード力がビーム要素に適用されます。

プリロードは、1方向、2方向、または3方向すべてに指定できます。

どの方向のプリロードのデフォルトもゼロです。つまり、ビームはデフォルトでは事前に荷重がかけられていません。

preload_tx, preload_ty, preload_tz

ビームに対するプリロードとして適用されるX、Y、またはZ軸に関するモーメントを定義します。X、Y、またはZ方向について計算されたモーメントに加えて、指定されたプリロードモーメントがビーム要素に適用されます。

プリロードは、1方向、2方向、または3方向すべてに指定できます。

どの方向のプリロードのデフォルトもゼロです。つまり、ビームはデフォルトでは事前に荷重がかけられていません。

例

これらの仕様に従ったForce_Beam定義は次のとおりです：

<Force_Beam
     id                  = "7"
     i_marker_id         = "37"
     j_marker_id         = "47"
     length              = "57.55"
     E                   = "200000."
     G                   = "76923.08."
     area                = "314.1593"
     ixx                 = "15707.96"
     iyy                 = "7853.982"
     izz                 = "7853.982"
     ASY                 = "1.2"
     ASZ                 = "1.2"
     cratio              = "0.001">
</Force_Beam>

コメント

1. ティモシェンコ梁では、せん断応力が面外せん断変形に及ぼす影響が考慮されますが、Euler-Bernoulli梁では考慮されません。ビームの高さ方向に対して、せん断は一定と見なされます。

   図 1 は、Force_Beam要素に関する定義を示しています。

2. J_Reference_Markerのx軸は、ビームの中立軸を定義します。J_Reference_Markerのy軸とz軸は、断面の主軸を定義します。言い換えると、これらの方向に沿った慣性乗積I_yzはゼロです。
3. 変形がゼロの状態で、I_Reference_Markerは、J_Reference_Markerのx軸に沿って、ビームの自由長に等しい距離だけオフセットされます。この向きはJ_Reference_Markerと同じです。

   以下の力がビームに作用します。

4. 軸力S1、S7。
   • せん断力S2、S3、S8、S9。
   • 曲げモーメントS5、S6、S11、S12。
   • ねじりモーメントS4、S10。

   
   
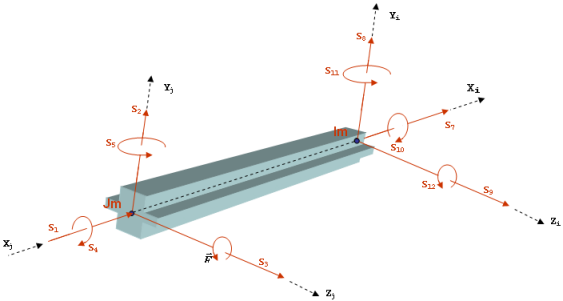
   図 1. Force_Beamの定義

5. 3つのたわみ角AX(I,J)、AY(I,J)、AZ(I,J)は、常に小さい必要があります。そうでない場合、角度AX()、AY()、AZ()は物理的意味を失い、梁理論は無効になります。小さいとは10度未満を意味します。
6. 剛性マトリクスは、以下の式に従って入力値から計算されます：
   (3)
   
   

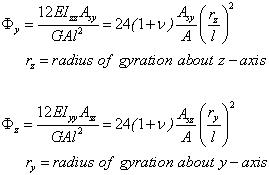
   (r_z/l) と(r_y/l)は、ビームの細長さの指標です。細長いビームの場合、この比は非常に小さいため、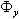と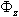はゼロと見なすことができます。このためには、A_syとA_szをゼロに設定します。

   剛性マトリクス（Przemieniecki, J.S、“Theory of Matrix Structural Analysis”、Dover Publications, Inc.、ISBN 0-486-64948-2、70-82ページ参照）は、物理特性から次のように計算できます：

   (4)

   $$K=\left[\begin{array}{cccccc}\frac{EA}{l}& 0& 0& 0& 0& 0\\ 0& \frac{12E{I}_{ZZ}}{l^3\left(1+{\Phi }_Y\right)}& 0& 0& 0& \frac{-6E{I}_{ZZ}}{l^2\left(1+{\Phi }_Y\right)}\\ 0& 0& \frac{12E{I}_{YY}}{l^3\left(1+{\Phi }_Z\right)}& 0& \frac{6E{I}_{YY}}{l^2\left(1+{\Phi }_Z\right)}& 0\\ 0& 0& 0& \frac{G{I}_{XX}}{l}& 0& \\ 0& 0& \frac{6E{I}_{YY}}{l^2\left(1+{\Phi }_Z\right)}& 0& \frac{\left(4+{\Phi }_Z\right)E{I}_{YY}}{l\left(1+{\Phi }_Z\right)}& 0\\ 0& \frac{-6E{I}_{ZZ}}{l^2\left(1+{\Phi }_Y\right)}& 0& 0& 0& \frac{\left(4+{\Phi }_Y\right)E{I}_{ZZ}}{l\left(1+{\Phi }_Y\right)}\end{array}\right]$$
7. IとJには、大きさが同じで向きが逆の力が作用しています。JとIの間は分離されており、力は分離ベクトルに沿って作用しないため、ボディIに作用するトルクは、ボディJに作用するトルクと同じではありません。
8. 力とトルクの符合規則は次のとおりです：
   • 正の力は、IとJのReference_Markerを遠ざけます。負の力は、IとJのReference_Markerを引き寄せます。
   • 正のトルクは、J Reference_Markerを基準にしてI Reference_Markerを反時計回りに回転させます。したがって、TX、TY、TZの正の値は、それぞれAX、AY、AZの値を増大させます。
9. Force_Beamは線形要素です。非線形の力の関係を定義する場合は、Force_FieldまたはForce_Vector_TwoBodyモデリング要素を使用してください。
10. Force_Beamでは、反り、非均質材、湾曲したビーム、断面が不均一なビームはモデル化されません。
11. 不均一な断面は、それぞれ異なる断面プロパティを持つビームのグループでモデル化します。
12. 図 2 は、2つのボディ間に作用するForce_Beamの立体分解図を示しています。この立体分解図を使用して、Force_Beamの実装について詳しく説明します。
    • 方程式1-4は、変形の計算方法を示しています。
    • 方程式5-6は、力の実装を定義します。
    • 残りの4つの方程式7-10は、Force_Beam要素によって生成された力とトルクが2つのボディに適用されることを示しています。

    
    
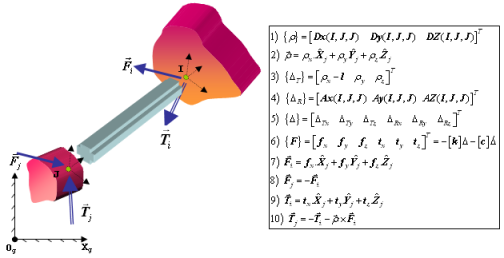
    図 2. Force_Beamの実装

13. ビームの断面が円形でない場合、ビームにねじり荷重がかかると、ビームがねじれます。このねじれによって端部が反り、放射状のラインは必ずしも直線のままになりません。このため、抵抗する断面のねじれは低減されます。よく使用される断面については、ねじり形状係数があらかじめ計算されています。

    詳細については、“Formulas for Stress and Strain”、Raymond J. RoarkおよびWarren C. Young、McGraw-Hill Book Company、ISBN 0-07-053031-9、290-296ページ、表20をご参照ください。

14. せん断スパン比が小さい、すなわち（r_z > 0.3L）または（r_y > 0.3L）であるビームの場合、せん断応力によって大きなたわみが生じる可能性があり、実際、せん断応力によって曲げ効果がほぼ決まる可能性があります。Force_Beamステートメント内の2つの係数ASYとASZでは、せん断たわみが考慮されます。以下の表は、鋳鉄の場合のASYとASZの標準値を示しています。

    断面

    ASYまたはASZ

    円形

    1.2

    矩形

    1.111（10/9）

    薄肉の中空円形断面

    2.0

    他の形状または材料のASYとASZを取得するには、“Formulas for Stress and Strain”、Raymond J. RoarkおよびWarren C. Young、McGraw-Hill Book Company、ISBN 0-07-053031-9、200-201ページ、表15をご参照ください。