Force: Penalty
Model ElementForce_Penaltyは、システム内での“ソフト”な拘束を維持することを目的とした、一般化力を定義します。
説明
これは、拘束が満たされていれば、ペナルティ力は存在しないことを意味します。ただし、拘束が侵されると、侵された分を縮小しようとするペナルティ力が生じます。一般化力は、拘束の定義に関与するすべての座標に作用します。
フォーマット
<Force_Penalty
id = "integer"
[label = "string"]
penalty = "double"
[penalty1 = "double"]
[[
unilateral = "False" | "True"
smoothing_factor = "real"
]]
{
type = "EXPRESSION"
expr = "motionsolve_expression"
type = "USERSUB"
usrsub_dll_name = "valid_path_name"
usrsub_fnc_name = "custom_fnc_name"
usrsub_param_string = "USER(par_1, ..., par_n)"
type = "USERSUB"
script_name = "valid_path_name"
interpreter = "PYTHON" | "MATLAB"
usrsub_fnc_name = "custom_fnc_name"
usrsub_param_string = "USER(par_1, ..., par_n)"
}
/>属性
- id
- 要素識別番号（整数 > 0）を指定します。この番号は、すべてのReference_Variable要素の中で一意です。
- label
- この属性は、Reference_Variable要素の名前を説明します。この説明は、主に、入力を読みやすくするために使用します。
- penalty
- 代数拘束が常にゼロとなるようにするために使用される復元力の計算に使用するペナルティ係数を指定します。penalty > 0。 2
- penalty1
- 代数拘束の時間微分を満足するために使用される復元力の計算に使用する2番目のペナルティ係数を指定します。penalty1のデフォルト値はゼロです。指定する場合は、penalty1 ≥ 0です。 3
- unilateral
- ブール属性。TRUEとFALSEのいずれかを選択します。等式拘束が指定されているのか、不等式拘束が指定されているのかを示します。unilateralはオプションの属性です。値を指定しない場合は、デフォルト値のFALSEが使用されます。 1 4
- smoothing_factor
- 片側拘束によるペナルティ力は、STEP関数を使用することで、滑らかに増加します。これは、平滑化が完了するxの値を指定します。smoothing_factor > 0。 4
- type
- EXPRESSIONまたはUSERSUBを選択します。ペナルティ力を制御する拘束の定義方法を指定します。
- EXPRESSION
- 実行時に評価できるMotionSolve式で拘束が定義されることを指定します。
- USERSUB
- ユーザー定義のサブルーチンで代数拘束が指定されることを示します。
- expr
- 代数拘束を定義するMotionSolveの式を指定します。この属性は、type = EXPRESSIONである場合にのみ使用します。任意の有効な実行時MotionSolve式を入力として指定できます。
- usrsub_dll_name
- ユーザーサブルーチンを含むDLLまたは共有ライブラリのパスと名前を指定します。MotionSolveはこの情報を使用して、実行時にDLL内のユーザーサブルーチンを読み込みます。このキーワードは、type = USERSUBの場合にのみ使用します。
- usrsub_fnc_name
- このパラメータにより、ユーザーサブルーチンの名前を指定できます。この属性が指定されない場合は、デフォルト名PFOSUBが使用されます。このキーワードは、type = USERSUBの場合にのみ使用します。
- usrsub_param_string
- データファイルからユーザー定義のPFOSUBに渡されるパラメータのリスト。このキーワードは、type = USERSUBの場合にのみ使用します。
- script_name
- usrsub_fnc_nameで指定された関数を含むユーザー作成スクリプトのパスと名前を指定します。このキーワードは、type = USERSUBの場合にのみ使用します。
- interpreter
- ユーザースクリプトが記述されたインタープリタ型言語を指定します。有効な選択肢は、MATLABまたはPYTHONです。このキーワードは、type = USERSUBの場合にのみ使用します。
例1
図 1に示すように、全体座標系xy平面に固定された懸垂線上を、粒子としてモデル化されたビーズが滑るとします。ビーズのパスを赤い円で示し、懸垂線を青いラインで示します。
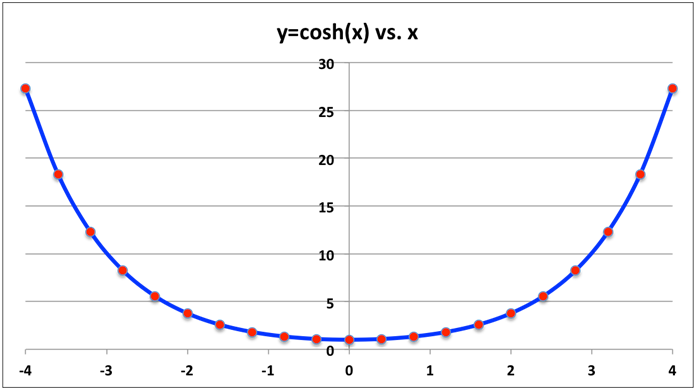
図 1. 懸垂線上を滑るビーズ
拘束は、g(x,y) = y - cosh(x) = 0と表されます。
拘束の時間導関数は、g(ẋ,ẏ,x,y) = ẏ - sinh(x)ẋ = 0となります。
MARKER 9が、ビーズの質量中心を表すとします。1E4のペナルティを使用して拘束を適用し、1E2のペナルティを使用して拘束の時間導関数を適用します。MotionSolveのForce_Penaltyステートメントは次のようになります：
<Force_Penalty
id = "1"
label = "Particle sliding on a catenary"
type = "EXPRESSION"
expr = "dy(9) - cosh(dx(9))"
penalty = "1E4"
penalty1 ="1E2"
/>ペナルティ力の変位拘束は次のようになります：
g = dy(9)-cosh(dx(9))ペナルティ力の速度拘束は次のようになります：
ġ= vy(9)-sinh(dx(9)*vx(9)MotionSolveにより計算されるペナルティ力は次のようになります：
F = -1E4*g - 1E2*ġ
= -1E4*[dy(9)-cosh(dx(9)] -1E2*[vy(9)-sinh(dx(9))*vx(9)]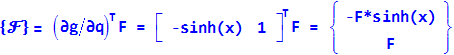
例2
この例は、Force_Penaltyを使用して、簡単な片側拘束を実装する方法を示しています。 図 2 は、マーカーJの座標系で定義されるラインL, y=1+xを示しています。
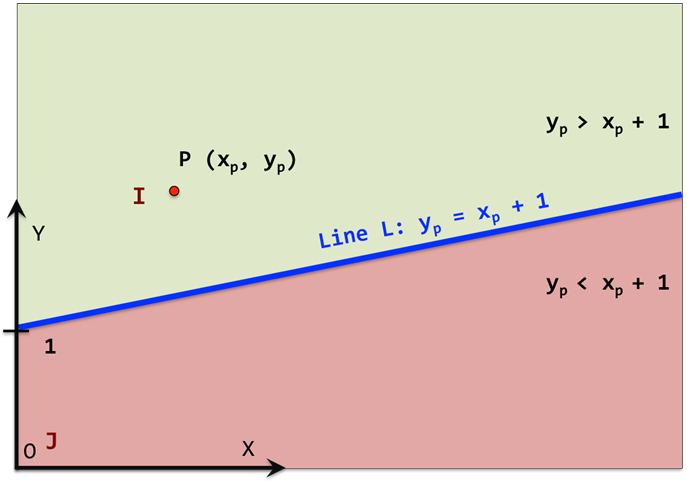
図 2. ライン上で跳ねる粒子P L: y=x+1
Jには、原点O、Xに沿ったx軸、およびYに沿ったy軸があります。別のボディに属するポイントPは、Jで測定される座標（xp、yp）を持ちます。便宜上、原点をPとするマーカーI=10を定義します。
- この要件を捕捉する不等式拘束を定義します。
- 貫入および貫入速度に依存する接触力を適用するためのForce_Penaltyを定義します。
簡単な座標形状についての考察から、次のようなことがわかります：
- 緑色の可動領域は次のように表されます： yp > 1 + xp
- 赤色の非可動領域は次のように表されます： yp < 1 + xp
- これらの領域の境界は次のラインで表されます： L: yp = 1 + xp
適用する拘束は次のようになります：yp ≥ 1 + xpまたは 1 + xp - yp ≤ 0
したがって、Force_Penalty定義は次のようになります：
<Force_Penalty
id = "10"
label = "Enforce 1+x < = y"
type = "EXPRESSION"
expr = "1 + dx(10) - dy(10)"
penalty = "1E4"
penalty = "1E2"
unilateral = "True"
smoothing_factor = "1.0"
/>例3
この例は、Force_Penaltyを使用して、簡単な片側拘束を実装する方法を示しています。 図 3 は、マーカーJの座標系で定義されるラインL, y=1+xを示しています。
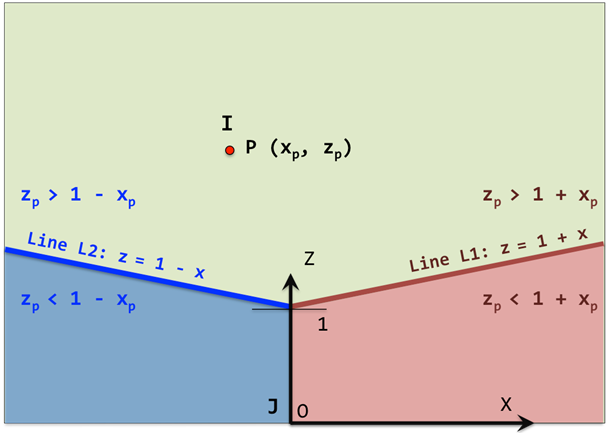
図 3. 2つのラインL1: z=1+xおよび間で跳ねる粒子P L2: z=1-x
- この要件を捕捉する不等式拘束を定義します。
- これらの拘束を適用するための2つのForce_Penaltyを定義します。
- L1より上の緑色の可動領域は次のように表されます： zp > 1 + xp
- L1より下の赤色の非可動領域は次のように表されます： zp < 1 + xp
- これらの領域の境界はラインL1で表されます： zp = 1 + xp
- L2より上の緑色の可動領域は次のように表されます： zp > 1 - xp
- L2より下の青色の非可動領域は次のように表されます： zp < 1 - xp
- これらの領域の境界はラインL2で表されます： zp = 1 - xp
- zp ≥ 1 + xpor1 + xp - zp ≤ 0
- zp ≥ 1 - xpor1 - xp - zp ≤ 0
したがって、Force_Penalty定義は次のようになります：
<Force_Penalty |<Force_Penalty
id = "1" | id = "2"
label = "Enforce 1+x<=z" | label = "Enforce 1-x<=z"
type = "EXPRESSION" | type = "EXPRESSION"
expr = "1+dx(10)-dz(10)" | expr = "1-dx(10)-dz(10)"
penalty = "1E4" | penalty = "1E4"
penalty1 = "1E2" | penalty1 = "1E2"
unilateral = "True" | unilateral = "True"
smoothing_factor = "1.0" | smoothing_factor = "1.0"
/> |/>図 4 は、粒子P（マーカー10）が初期状態Xp=100 mmおよびZp=120 mmから開始し、重力により落下するときの、XおよびZ座標を示しています。重力加速度は、Z方向に-9810 mm/s2です。
粒子はこの2つのライン間ではずみ、最終的にZp=1、Xp=0で止まります。
図 4. 2つのラインL1: z=1+xおよび間ではずむ粒子PのZおよびXの時刻歴 L2: z=1-x
コメント
- Force_Penaltyを使用して、片側拘束または不等式拘束を定義できます。qを、システム変位に依存する任意の値セットとします。
- 等式拘束または両側拘束は次のようになります： g(q,t) = 0
- 不等式拘束または片側拘束は次のようになります： g(q,t) ≤ 0
- どちらの場合も、次のように拘束が侵された場合にのみペナルティ力が生じます。
- 等式拘束の場合： g(q,t) ≠ 0
- 片側拘束の場合： g(q,t) > 0
- 拘束g(q,t)=0は、モデル内で維持されるものとします。
この問題を解析する手法の1つに、ユーザー定義の拘束を定義し、その拘束g(q,t)=0をMotionSolveに指定する方法があります。この拘束は、残りのシステム変数によって求められる未知のLagrange乗数λによって適用されます。
- λは力またはトルクです。
- λは、拘束の勾配
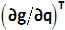に沿って作用します。 - システムに作用する一般化力は、
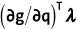となります。 上記手法の詳細については、Constraint_Generalをご参照ください。
Force_Penaltyでは、やや異なる方法を使用して、同じ解析を実施します。拘束は“ソフト”であり、厳しく適用されるものではありません。拘束を侵すことは可能ですが、拘束違反を減少させようとする復元力が、内部的に生成されます。
- ペナルティ力は力またはトルクです。
- ペナルティ力の大きさは、F = -penalty*g(q,t)となります。
- ペナルティ力は、拘束の勾配
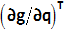に沿って作用します。 - システムに作用する一般化力は、
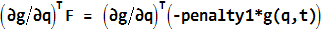となります。 - 一般的には、penaltyが大きいと、拘束違反は小さくなります。
Lagrange乗数によるハード拘束とペナルティ力によるソフト拘束は密接に対応しています。
- g(q,t)=0である場合、これはそのままġ(q̇,,q,t)=0であることを意味します（ġ(...) =
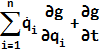）。q̇は、qに対応する速度です。ġ(q̇,,q,t)=0を適用するには、2番目の成分-penalty1*ġ(q̇,,q,t)を前に計算したペナルティ力に追加する必要があります。g(q,t)=0とġ(q̇,,q,t)=0の両方を適用するには、次の方法を使用します：- ペナルティ力の大きさは、F = -penalty*g(q,t) - penalty1*ġ(q̇,,q,t)となります。
- ペナルティ力は、拘束の勾配
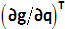に沿って作用します。 - システムに作用する一般化力は、
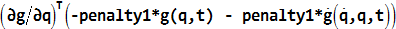となります。 penalty1が指定されている場合、MotionSolveは、運動方程式で上記の式を使用してペナルティ力と一般化力を計算します。
- 平滑化関数を使用すると、3の式が次のように平滑化されます：
- p = penalty * STEP(g(q),0,0,smoothing_factor,1)
- p1 = penalty * STEP(g(q),0,0,smoothing_factor,1)
- F = - p*g(q,t) - p1*ġ(q̇,,q,t) )
- STEP関数を使用すると、違反が増加するにつれ、ペナルティ係数が徐々に増加します。これを図 5に示します。平滑化係数が小さくなると、遷移は急勾配になります。
図 5. 片側拘束での平滑化係数 - 関数g(y,t)を定義するには、次の3つの手法を使用できます。
- XMLファイル内の関数式として：これは最も簡単な方法であり、関数式言語に組み込まれた関数と演算子で構成された式としてg(y,t)が定義されます。
- DLLで指定されるユーザー作成のコンパイルされたサブルーチンとして：任意の言語を使用できます。MotionSolveでは、Fortran、C、およびC++のインターフェースを用意しています。ユーザー作成のサブルーチンのデフォルト名はPFOSUBです。ただし、この関数に任意の名前を付け、MotionSolveにその名前を伝えることができます。
- PythonまたはMATLAB言語で記述されたスクリプトとして：この手法は、コンパイルされた言語でユーザー作成のサブルーチンを記述するより若干効率は下がりますが、次の2つの大きな利点があります：（A）関数g(y,t)を構成するために、関数式に比べてはるかに柔軟で強力な環境を提供します。（B）Fortran、C、またはC++を使用する場合に、コンパイラやリンカーが必要ありません。
- penaltyおよびpenalty1に過度に大きな値を使用すると、数値的な問題が生じる場合があります。penaltyは剛性と同程度、penalty1は減衰と同程度とお考えください。
- smoothing_factorに非常に小さな値を使用しても、数値的な問題が生じる場合があります。確かな経験則として、平滑化係数を、予測される最大貫入の一部分程度にすることをお勧めします。
- h(q,t) ≥
0の形の拘束は、次のように実装できます。
- 以下のように定義します： g(q,t) = -h(q,t)
- 以下に対してペナルティ拘束を適用します： g(q,t) ≤ 0