Force: State Equation
Model ElementForce_StateEqnは、Control_StateEqnとForce_Vector_TwoBodyのモデリング要素のモデリング機能を結合する抽象的モデリング要素です。
説明
Force_StateEqnはベクトル力(FX、FY、FZ、TX、TY、およびTZ)の適用に使用され、出力数はちょうど6になります。
- 入力ベクトル u
- 一連の微分方程式を介して定義される動的状態のベクトルx
- 一連の代数方程式で定義される出力ベクトルyForce_StateEqnはベクトル力(FX、FY、FZ、TX、TY、およびTZ)の適用に使用されるため、出力数は6に固定されます。
下の図は、動的システムの基本概念を示しています。

図 1. 動的システムの入力、出力および状態
このような動的システムでは、uが与えられると、Force_StateEqnが状態ベクトルxを計算し、出力yをベクトル力として2つの指定されたボディ間に適用します。
Control_StateEqnと同様、MotionSolveでは2つのタイプのForce_StateEqn要素が使用可能です。
- 線形動的システム:これらは4つのマトリクスA、B、C、Dで表現されます。これらは、次のように動的システムに関連付けられます: 4つのマトリックスA, B, C, Dはすべて定数値です。最初の式は状態を定義し、2番目の式は出力を定義します。
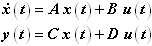
図 2.Aマトリクスは状態マトリクスと呼ばれ、システムの特性を定義します。“n”個の状態がある場合、Aマトリクスの次元はn x nとなります。Aは正則である必要があります。
Bマトリクスは入力マトリクスと呼ばれ、入力が状態に与える影響を定義します。“m”個の入力がある場合、Bマトリクスのサイズはn x mとなります。Cマトリクスは出力マトリクスと呼ばれ、状態が出力に与える影響を定義します。“p”個の出力がある場合、Cマトリクスのサイズはp x nとなります。
Dマトリクスは直接フィードスルーマトリクスと呼ばれ、入力が直接出力に与える影響を定義します。Dマトリクスのサイズはp x mとなります。 - 非線形動的システム:これらは、F()とG()の2つのベクトル関数で表現されます。これらは、次のように動的システムに関連付けられます: 関数F()は、x(t)とu(t)が与えられると、xの時間導関数を返します。関数G()は、x(t)とu(t)が与えられると、出力yを返します。F()とG()はどちらも、ユーザー定義のサブルーチンで定義する必要があります。
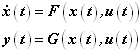
図 3.
フォーマット
<Force_StateEqn
id = "integer"
[ label = "string" ]
x_array_id = "integer"
ic_array_id = { "integer" | "0" }
[ is_static_hold = { "TRUE" | "FALSE" } ]
i_marker_id = "integer"
j_floating_marker_id = "integer"
ref_marker_id = "integer"
[ u_array_id = "integer" ]
{
type = "LINEAR"
a_matrix_id = "integer"
[ b_matrix_id = "integer" ]
[ c_matrix_id = "integer" ]
[ d_matrix_id = "integer" ]
| type = "USERSUB"
num_state = "integer"
usrsub_param_string = "USER( [[par_1][, ...][, par_n]] )"
usrsub_dll_name = "valid_path_name"
[ usrsub_fnc_name = "custom_fnc_name" ]
[ usrsub_der1_name = "custom_fnc_name" ]
[ usrsub_der2_name = "custom_fnc_name" ]
[ usrsub_der3_name = "custom_fnc_name" ]
[ usrsub_der4_name = "custom_fnc_name" ]
| type = "USERSUB"
num_state = "integer"
script_name = valid_path_name
interpreter = "PYTHON" | "MATLAB"
usrsub_param_string = "USER( [[par_1 [, ...][,par_n]] )"
[ usrsub_fnc_name = "custom_fnc_name" ]
[ usrsub_der1_name = "custom_fnc_name" ]
[ usrsub_der2_name = "custom_fnc_name" ]
[ usrsub_der3_name = "custom_fnc_name" ]
[ usrsub_der4_name = "custom_fnc_name" ]
>
}
</Force_StateEqn>属性
- id
- 要素識別番号(整数 > 0)。これは、すべてのForce_StateEqn要素の中で一意の番号です。
- label
- Force_StateEqn要素の名前。
- is_static_hold
- 静的平衡解析および擬似静解析の間、動的状態の値xを固定するかどうかを指定するブール値。
- “TRUE”
- 静解析および擬似静解析の間、動的状態が一定に保たれることを意味します。
- "FALSE"
- 静的平衡解析または擬似静解析の間、動的状態が変化可能であることを意味します。
- i_marker_id
- 力が適用されるReference_Markerを指定します。これは力の作用点として指定されます。
- j_floating_marker_id
- 同じ大きさで反対向きの反力が適用されるReference_Markerを指定します。このマーカーは、i_marker_id上に常に重ね合わされるよう、親ボディ上で移動されます。このような構成により、ニュートンの第三法則を自動的に満たすことができます。j_floating_marker_idは、剛体または質点のみに属することができます。弾性体の一部になることはできません。
- ref_marker_id
- 力ベクトルの成分を定義する基準として使用する座標系を持つReference_Markerを指定します。
- x_array_id
- このForce_StateEqnの状態“x”を格納するために使用するReference_ArrayのIDを指定します。このIDを持つARYVAL()関数を使用することで、MotionSolveの式でこの状態にアクセスすることができます。また、SYSFNCおよびSYSARYでこのIDを使用することで、ユーザーサブルーチンの状態値にアクセスすることもできます。
- u_array_id
- このForce_StateEqnの入力uを格納するために使用するReference_ArrayのIDを指定します。このIDを持つARYVAL()関数を使用することで、MotionSolveの式でこの状態にアクセスすることができます。また、SYSFNCおよびSYSARYでこのIDを使用することで、ユーザーサブルーチンの入力値にアクセスすることもできます。
- ic_array_id
- このForce_StateEqnの状態xの初期値を格納するために使用するReference_ArrayのIDを指定します。このIDを持つARYVAL()関数を使用することで、MotionSolveの式でこの状態にアクセスすることができます。また、SYSFNCおよびSYSARYでこのIDを使用することで、ユーザーサブルーチンの初期状態値にアクセスすることもできます。
- type
- モデル化する動的システムのタイプを指定します。“LINEAR”と“USERSUB”のいずれかを選択します。
- "LINEAR"
- モデル化している動的システムが線形であることを指定します。このシステム定義を行うには、A、B、C、DのマトリクスのIDを指定します。
- “USERSUB”
- モデル化している動的システムがユーザー定義のサブルーチンで定義されることを指定します。この動的システムは線形でも非線形でもかまいません。
- a_matrix_id
- 線形のForce_StateEqnの状態マトリクスを含むReference_MatrixオブジェクトのIDを指定します。Aマトリクスは、動的システムの固有のプロパティをカプセル化します。例えば、Aの固有値は、システムの固有値を表します。同様に、Aの固有ベクトルは、動的システムのモード形状を表します。Aは定数値のマトリックスです。これは正則である必要があります。n個の状態がある場合、Aマトリックスの次元はn x nです。type = "LINEAR"の場合にのみ使用します。
- b_matrix_id
- 線形のForce_StateEqnの入力マトリックスを含むReference_MatrixオブジェクトのIDを指定します。Bマトリックスは、入力uの状態方程式への寄与を決定します。
- c_matrix_id
- 線形のForce_StateEqnの出力マトリックスを含むReference_MatrixオブジェクトのIDを指定します。Cマトリックスは、状態xの出力yへの寄与を決定します。Cは定数値のマトリックスです。p個の出力とn個の状態がある場合、Cマトリックスの次元はn x pとなります。
- d_matrix_id
- 線形のForce_StateEqnのフィードスルーマトリックスを含むReference_MatrixオブジェクトのIDを指定します。Dマトリックスは、入力uの出力yへの寄与を決定します。Dは定数値のマトリックスです。p個の出力とm個の入力がある場合、Dマトリックスの次元はp x mとなります。
- num_state
- Force_StateEqnの状態の数を指定する整数。num_state > 0。
- usrsub_param_string
- データファイルからユーザー定義のサブルーチンYFOSUB、YFOXX、YFOXU、YFOYX、およびYFOYUに渡されるパラメータのリスト。これらのユーザー定義サブルーチンの詳細については、コメント4をご参照ください。type = "USERSUB"の場合にのみ使用します。この属性は、すべてのタイプのユーザーサブルーチンおよびスクリプトに共通です。
- usrsub_dll_name
- ユーザーサブルーチンを含むDLLまたは共有ライブラリのパスと名前を指定します。MotionSolveはこの情報を使用して、実行時にDLL内のユーザーサブルーチンYFOSUB、YFOXX、YFOXU、YFOYX、およびYFOYUを読み込みます。type = "USERSUB"の場合にのみ使用します。
- usrsub_fnc_name
- ユーザーサブルーチンYFOSUBの代替名を指定します。
- usrsub_der1_name
- ユーザーサブルーチンYFOXXの代替名を指定します。
- usrsub_der2_name
- ユーザーサブルーチンYFOXUの代替名を指定します。
- usrsub_der3_name
- ユーザーサブルーチンYFOYXの代替名を指定します。
- usrsub_der4_name
- ユーザーサブルーチンYFOYUの代替名を指定します。
- script_name
- usrsub_fnc_nameで指定されたルーチンを含むユーザー作成スクリプトのパスと名前を指定します。
- interpreter
- ユーザースクリプトが記述されたインタープリタ型言語を指定します。有効な選択肢は、MATLABまたはPYTHONです。
例

図 4. 単純な振り子システム
このモデルは2次元の問題を示しています。このシステムは、剛性の質量のないロッドに固定される単一質量で構成されます。ロッドは、全体座標系Y軸の周りでのみ回転できる回転ジョイントを介して地面に結合されています。スプリングのおもりの質量は1kgで、質量のないロッドの長さは100mmです。負のZ方向に重力が適用されます。ロッドと全体座標系Z軸の間の角は、 と表され、式AZ(30101020,30102020)によりモデル内で測定されます。
- 振り子のおもりは、最初は止まっています。初期角度 は90度で、振り子は水平の状態です。
- 重力により、振り子のおもりが、XZ平面内で全体座標系Y軸の周りを回転しながら自由に揺れます。
- 摩擦トルクTfは、ヒンジの結合部分で振り子の回転と反対向きに作用し、その結果、しばらくしてから振り子は止まります。
このモデルの設計パラメータは次のとおりです:
この例で、Force_StateEqn要素は以下のようになります:
<Force_StateEqn
id = "301001"
type = "USERSUB"
x_array_id = "535050504"
y_array_id = "535050508"
u_array_id = "535050505"
num_state = "2"
num_output = "6"
usrsub_param_string = "USER(1001,100.,0.31625,0.0004,1.,5.,1.5,1.25,0.5,0.3,0.)"
usrsub_dll_name = "ms_csubdll"
usrsub_fnc_name = "YFOSUB"
is_static_hold = "FALSE"
i_marker_id = "30101020"
j_floating_marker_id = "30102020"
ref_marker_id = "30102020"
/>Iマーカーは次のように定義されます:
<Reference_Marker
id = "30101020"
label = "Pivot-Marker I"
body_id = "30101"
body_type = "RigidBody"
a00 = "-1."
a10 = "0."
a20 = "0."
a02 = "0."
a12 = "1."
a22 = "0."
/>X、Y、およびU配列は、次のように定義されます:
<Reference_Array
id = "535050504"
type = "X"
num_element = "2"
/>
<Reference_Array
id = "535050508"
type = "Y"
num_element = "6"
/>
<Reference_Array
id = "535050505"
type = "U"
num_element = "7"
usrsub_param_string = "USER(1001,301001)"
usrsub_dll_name = "ms_csubdll"
usrsub_fnc_name = "ARYSUB"
/>U配列には7つの値(振り子の角速度、および6つのジョイント反力)が含まれます。これは、下のARYSUBのコードを見るとよくわかります。
以下に、ユーザーサブルーチンYFOSUBおよびARYSUBで使用されるコードを示します:
DLLFUNC void STDCALL YFOSUB (int *id, double *time, double *par, int *npar,
int *dflag, int *iflag, int *nstate, double *states,
int *ninput, double *input, int *noutpt, double *stated,
double *output)
{
/*
# YFOSUB evaluates the f and g in the following general state eqn
# x' = f(x,u,t)
# y = g(x,u,t)
# where x is the states, x' is the stated, u is the input, and y the output.
# The output (y) is used as the force acting between the i and j markers.
*/
if (int(par[0])==1001) // Joint Friction (Revolute)
{
// Parameter list for Joint Friction with Revolute Joints
// (joint_id,sigma0,sigma1,sigma2,vS,Rb,Rp,Rf,muS,muD,Preload)
double sigma0 = par[1]; // LuGre parameter
double sigma1 = par[2]; // LuGre parameter
double sigma2 = par[3]; // LuGre parameter
double vS = par[4]; // Stribeck velocity
double Rb = par[5]; // Bending arm
double Rp = par[6]; // Pin Radius
double Rf = par[7]; // Friction arm
double muS = par[8]; // Static coefficient of Friction
double muD = par[9]; // Dynamic coefficient of Friction
double Preload = par[10]; // Friction Preload
// Joint Reactions
int i;
double jReact[6];
for(i=0;i<6;i++)
{
jReact[i] = input[i+1];
}
double Fr = pow((pow(jReact[0],2) + pow(jReact[1],2)),0.5);
double Fa = jReact[2];
double Fb = jReact[3]/Rb + jReact[4]/Rb;
// Compute slip velocity
double vSlipR = input[0]*Rp;
double vSlipA = input[0]*Rf;
// Compute Stribeck and Coulomb Force levels
double FCr = muD;
double FSr = muS;
double FCa = muD;
double FSa = muS;
// GSE stuff
double rExp = pow(2.718,(-pow((vSlipR/vS),2)));
double aExp = pow(2.718,(-pow((vSlipA/vS),2)));
double GVr = (FCr + (FSr - FCr)*rExp)/sigma0;
double GVa = (FCa + (FSa - FCa)*aExp)/sigma0;
stated[0] = vSlipR;
stated[1] = vSlipA;
if (fabs(GVr)>1e-12)
{
stated[0] -= states[0]*fabs(vSlipR)/GVr;
}
if (fabs(GVa)>1e-12)
{
stated[1] -= states[1]*fabs(vSlipA)/GVa;
}
// Friction Torque
double FTrqR = (Fr+Fb+Preload)*Rp*(sigma0*states[0] + sigma1*stated[0] + sigma2*vSlipR);
double FTrqA = (Fa)*Rf*(sigma0*states[1] + sigma1*stated[1] + sigma2*vSlipA);
output[0] = 0.0;
output[1] = 0.0;
output[2] = 0.0;
output[3] = 0.0;
output[4] = 0.0;
if (vSlipR<0)
{
output[5] = fabs(FTrqR + FTrqA);
}
else
{
output[5] = -fabs(FTrqR + FTrqA);
}
}
}
/*DLLFUNC void STDCALL ARYSUB (int *id, double *time, double *par,
int *npar, int *dflag, int *iflag, int *nvalue, double *value)
{
if (((int)par[0])==1001)
{
int errflg = 0;
int ipar[4];
int joint_id = (int)par[1];
int i_marker;
int j_marker;
char imark[80],jmark[80];
//Get the I and J marker ID for the joint
c_modfnc("Constraint_Joint",joint_id,"i_marker_id",imark,&errflg);
c_modfnc("Constraint_Joint",joint_id,"j_marker_id",jmark,&errflg);
i_marker = atoi(imark);
j_marker = atoi(jmark);
ipar[0] = i_marker;
ipar[1] = j_marker;
ipar[2] = j_marker;
//Query the solver for angular velocity using WZ(I, J, J)
c_sysfnc("WZ", ipar, 3, &value[0], &errflg);
ipar[0] = joint_id;
ipar[1] = 0;
ipar[2] = 2;
ipar[3] = j_marker;
//Get the Joint reaction forces - these will be used as input to the YFOSUB
c_sysfnc("JOINT", ipar, 4, &value[1], &errflg);
ipar[2] = 3;
c_sysfnc("JOINT", ipar, 4, &value[2], &errflg);
ipar[2] = 4;
c_sysfnc("JOINT", ipar, 4, &value[3], &errflg);
ipar[2] = 6;
c_sysfnc("JOINT", ipar, 4, &value[4], &errflg);
ipar[2] = 7;
c_sysfnc("JOINT", ipar, 4, &value[5], &errflg);
ipar[2] = 8;
c_sysfnc("JOINT", ipar, 4, &value[6], &errflg);
}
}
図 5. 回転ジョイントでの摩擦の有無による角変位の比較
コメント
- Force_StateEqn要素は、Control_StateEqn(GSE成分)モデリング要素とForce_Vector_TwoBody(力成分)要素を組み合わせたものと等価です。(入力を指定すると)GSE成分により状態および出力ベクトルが計算され、FORCE成分によりGSEからの出力が力およびトルクとしてi_marker_idで指定されたボディに適用され、反力および反トルクとしてj_floating_marker_idで指定されたボディに適用されます。
- Control_StateEqnと同様、Force_StateEqnも“LINEAR”および“USERSUB”バージョンで使用可能です。これらの詳細については、Control_StateEqnに関するドキュメントをご参照ください。
- Force_StateEqnの“USERSUB”バージョンは、ユーザー定義サブルーチンで定義されるほとんどのモデリング要素より複雑です。
5つのユーザーサブルーチンが必要となることがあります。まず、YFOSUBが必要です。残りの4つ、YFOXX、YFOXU、YFOYX、YFOYUは、stiff積分器(VSTIFFまたはMSTIFF)が使用される場合にのみ必要となります。
名前 入力 出力 YFOSUB 状態 - x 入力 - u
状態微分方程式、 出力、
YFOXX 状態 - x 入力 - u
偏導関数のマトリックス(n x n)、 YFOXU 状態 - x 入力 - u
偏導関数のマトリックス(n x m)、 YFOYX 状態 - x 入力 - u
偏導関数のマトリックス(p x n)、 YFOYU 状態 - x 入力 - u
偏導関数のマトリックス(p x n)、 - 静解析および擬似静解析の間のForce_StateEqn要素に関連する動的状態の挙動は、属性is_static_holdによって制御されます。is_static_hold = "TRUE"
時間T=0で解析が行われる場合、状態は、IC配列によって指定された値で固定されたままです。動的シミュレーションに続いて解析が行われる場合、値は動的シミュレーションから取得された最後の値で固定されたままです。Force_StateEqnの状態を定義する方程式は、以下に置き換えられます:
x(t*) = x*、ここでx*は定数です。注: 動的状態が固定されたままの場合、その時間導関数は、入力u(一般的に時間に依存する)が変化しているため、静的平衡または擬似静的ステップの最後でゼロにはならなくなります。これにより、その後動解析が実行される場合、過渡応答になる可能性があります。is_static_hold = "FALSE"
解析プロセスの間、状態は一定に保たれず、システム全体のコンフィギュレーションの変化に従って変えることができます。これがどのように実現されるかを以下に示します。
静解析および擬似静解析では、動的状態の導関数はゼロに設定されます。これにより、Force_StateEqnのGSE成分が、一連の代数方程式に変換されます。
微分方程式は次のようになります:
(1) 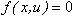
平衡解析では、システムのコンフィギュレーションが変化すると、平衡条件を満たすように入力uが変化します。上記の式が解かれ、現在のuの値に対するxが計算されます。
この方法により、動的状態の時間導関数が、静解析または擬似静解析の最後でゼロになり、その後の動的シミュレーションで過渡応答が生じるのを回避できます。