Parameters: Transient Solver

Model ElementParam_Transientは、時間領域に基づいた非線形動解析のシミュレーション制御パラメータを定義します。

説明

これらのパラメータは以下を制御します：

積分器の選択。
積分誤差トレランス（または解の精度）。
シミュレーション時の積分器のパフォーマンス。

動的シミュレーションは、自由度が1以上のシステムに対して実行されます。動的シミュレーションでは、すべての慣性の影響、すべての適用される力、および内部拘束が考慮されます。これによって、複雑な機構システムの正確なシステムレベルのシミュレーションが実行可能となります。

Param_Transientは、次の2つのカテゴリの方程式定式化をサポートしています：

微分代数方程式（DAE）形式の方程式。これは、多くの場合、より正確で、堅牢で、効率的なシミュレーションにつながるMotionSolve内のデフォルト定式化です。
常微分方程式（ODE）形式の方程式。これは、古い定式化で、古いモデルとの下位互換性をサポートするために含まれています。

フォーマット

<Param_Transient
 [ integrator_type = "string" ]
 [ integr_tol = "real" ]
 [ h_max = "real" ]
 [ h_min = "real" ]
 [ h0_max = "real" ]
 [ vel_tol_factor = "real" ]
 [ max_order = "integer"]
 [ dae_alg_tol_factor = "real" ]
 [ dae_index = "integer"]
 [ dae_constr_tol = "real" ]
 [ dae_corrector_maxit = "real" ]
 [ dae_corrector_minit = "real" ]
 [ dae_vel_ctrl = "TRUE|FALSE"]
 [ dae_jacob_eval = "integer"]
 [ dae_eval_expiry = "integer"]
 [ dae_jacob_init = "integer"]
 [ dae_interpolation = "TRUE|FALSE"]
/>

属性

integrator_type

ODE形式の運動方程式で使用される積分器を定義します。次のいずれかを選択します：

積分器	方程式の形式	タイプ	最大次数
DSTIFF	DAE	可変のステップと次数	5
CSTIFF	DAE	固定のステップと次数	5
VSTIFF	ODE	可変のステップと次数	5
MSTIFF	ODE	可変のステップと次数	9
ABAM	ODE	可変のステップと次数	12

integrator_typeのデフォルト値はDSTIFFです。これらの積分器の詳細については、後出のコメントをご参照ください。

integr_tol

積分器が変位、速度、微分方程式の状態を計算する際に許容されるステップあたりの最大絶対誤差を表します。

変位と速度の単位は異なるため、これらには異なる誤差トレランスが適用されます。

変位のトレランス = integr_tol
速度のトレランス = vel_tol_factor*integr_tol
微分方程式の状態のトレランス = integr_tol
代数状態のトレランス = dae_alg_tol_factor *integr_tol（DAEのみ）

integr_tolのデフォルト値は1.0E-3です。

vel_tol_factorは、別個に指定するスケールファクターです。

積分器タイプがCSTIFFの場合は、この属性が監視目的にのみ使用されます。MotionSolveは、測定された誤差が上記トレランスのいずれかを上回った段階でメッセージを出力します。

h_max

積分器で許容される最大ステップサイズを定義します。このパラメータを使用して、結果の精度を制御することもできます。一般に、時間ステップが小さいほど、結果の精度が高まります。非連続性があるモデルの場合（接触など）、h_maxに小さい値を指定する必要があります。

h_maxのデフォルト値は1.0E-3です。

積分器タイプがCSTIFFの場合は、h_maxで固定ステップが定義されます。

注: print_intervalがh_maxより小さい場合は、Simulateコマンドで最大積分器ステップサイズがprint_intervalに設定されます。

h_min

積分器で許容される最小ステップサイズを定義します。

h_minのデフォルト値は1.0E-6です。

積分器タイプがCSTIFFの場合は、この属性が無視されます。

h0_max

最大初期ステップサイズ。

h0_maxのデフォルト値は1.0E-8です。

積分器タイプがCSTIFFの場合は、この属性が無視されます。

vel_tol_factor

速度状態の誤差トレランスを得るため、integr_tolと掛け合わせる係数。

vel_tol_factorのデフォルト値は1000です。vel_tol_factorに適した値は、一般に1/hとして計算できます。hはシミュレーションの主なステップサイズです。解析時間を削減するには、デフォルトの1000より大きな値を使用します。ただし、これによってモデルの速度状態についての精度が低下します。

rel_abs_tol_ratio

積分器の相対誤差トレランスを得るため、integr_tolと掛け合わせる係数。

デフォルトの値は0.01。

積分器タイプがCSTIFFの場合は、この属性が監視目的にのみ使用されます。MotionSolveは、測定された誤差が相対誤差トレランスを上回った段階でメッセージを出力します。

max_order

積分器で使用される最高次数を指定します。各積分器には、独自の最高次数が組み込まれています。次数が高いほど精度が高まりますが、数値的手法での安定性は低下します。上の表に、MotionSolve内のさまざまな積分器の最大次数を示します。接触などの非連続イベントを含むモデルの場合は、max_order = 2に設定することをお勧めします。

積分器タイプがCSTIFFの場合は、max_orderで固定次数が定義されます。

属性（DAEソルバーに固有）

dae_alg_tol_factor

Lagrange乗数のような代数状態の誤差トレランスを得るため、integr_tolと掛け合わせる係数。

dae_alg_tol_factorのデフォルト値は1000です。

dae_index

DAE定式化のインデックス。

インデックス3は、位置の拘束が運動方程式に追加されることを示します。

インデックス1は、位置、速度、および加速度の拘束が追加されることを示します（安定化されたインデックス1）。

詳細については、コメント2～3をご参照ください。

dae_indexのデフォルト値は3です。

dae_constr_tol

収束時に修正子が満たす必要のあるすべての代数拘束方程式のトレランス。

dae_constr_tolのデフォルト値は1.0E-5です。ジョイントまたはモーションの反力で多くの“ノイズ”が見られる場合にのみ、この値を小さくします。この属性の値が小さいほど、解析速度が低下します。 12

積分器タイプがCSTIFFの場合は、この属性が監視目的にのみ使用されます。MotionSolveは、測定された誤差が代数拘束トレランスを上回った段階でメッセージを出力します。

dae_corrector_maxit

収束を達成するために修正子が実行できる反復計算の最大回数。

dae_corrector_maxit のデフォルト値は4です。いかなる場合も、この値を8より大きい値にしないでください。特定の時間ステップで結果が収束しない場合は、積分器を失敗させて、より小さい時間ステップで解析を試行することをお勧めします。

積分器タイプがCSTIFFの場合は、dae_corrector_maxitで各時間ステップ内の固定反復回数が定義されます。

dae_corrector_minit

修正子が実行する反復計算の最少回数。この回数に達すると、修正子の発散が生じていないかチェックされます。

dae_corrector_minitのデフォルト値は0です。値を0にすると、積分器が反復計算の最少回数を選択します。指定のステップについてノルムがトレランスより小さい場合、積分器は修正子の反復計算をスキップすることもできます。

いかなる場合も、この値を3より大きい値にしないでください。

積分器タイプがCSTIFFの場合は、この属性が無視されます。

dae_vel_ctrl

各ステップで局所積分誤差が生じていないかを確認するために速度状態をチェックするかどうかを制御する論理フラグ。これはSI1積分器にのみ有効です（dae_indexをご参照ください）。

“TRUE”の場合、積分器は、各ステップの最後に実行される局所積分の有無のチェックに速度状態を含めます。
“FALSE”の場合、積分器は、各ステップの最後に実行される局所積分の有無のチェックに速度状態を含めません。

指定しない場合のデフォルト値は、SI1定式化の場合は“TRUE”、I3定式化の場合は“FALSE”です。定式化の詳細については、コメント4～6をご参照ください。

積分器: DAE_VEL_CTRL
I3定式化: “FALSE”
SI1定式化: "TRUE"

I3定式化は、速度誤差を追跡するように設計されていません。したがって、I3についてDAE_VEL_CTRLが“TRUE”の場合でも、速度誤差は追跡されません。

dae_jacob_eval

この属性は、修正子の反復計算時にヤコビアンマトリクスの評価の頻度を制御します。

0: 積分器は収束速度を調べることで、新しいヤコビアンが必要なタイミングを自動的に特定します。
1: 反復計算ごとに新しいヤコビアンが計算されます。
2: 1つおきの反復計算で新しいヤコビアンが計算されます（例：反復計算1-3-5など）。
3: 2つおきの反復計算で新しいヤコビアンが計算されます（例：反復計算1-4-7など）。

デフォルト設定がうまく機能しない場合にのみ、dae_jacob_evalを指定してください。ヤコビアン反復計算の頻度が高いと、シミュレーション速度が大幅に低下する可能性があります。

指定しなかった場合、積分器は収束速度を調べることで、新しいヤコビアンが必要なタイミングを自動的に特定します。

ヤコビアンの評価は、属性dae_jacob_initの影響も受けます。 13

積分器タイプがCSTIFFの場合は、dae_jacob_evalを1以上にする必要があります。

dae_eval_expiry

これはオプションの属性です。積分ステップの数を指定します。この数の積分ステップの後は、dae_jacob_evalで定義された評価パターンが無視され、デフォルトの評価パターンが使用されます。修正子の収束速度を調べることで、新しいヤコビアンが必要になると、デフォルトの評価パターンが自動的に特定されます。

例えば、dae_eval_expiry = "10"と設定した場合、10個の積分ステップが正常に実行された後は、dae_jacob_evalで指定されたパターンが無視されます。

dae_eval_expiryのデフォルト値は0です。これは、シミュレーション全体にわたってdae_jacob_evalで指定されたパターンが使用されることを意味します。

このフラグは、システム内の初期の過渡現象に対処するためだけにdae_jacob_evalを適用したい場合に使用します。

積分器タイプがCSTIFFの場合は、この属性が無視されます。

dae_jacob_init

この属性は、修正子の反復計算時の初期ヤコビアンマトリクスの評価数を指定します。

0: 積分器は収束速度を調べることで、新しいヤコビアンが必要なタイミングを自動的に特定します。
1: 最初の反復計算で新しいヤコビアンが計算され、その後は計算されません。
2: 最初と2番目の反復計算で新しいヤコビアンが計算され、その後は計算されません。ここに3以上の値を設定した場合も同様です。

デフォルト = 0

積分器タイプがCSTIFFの場合は、dae_jacob_initを1以上にする必要があります。

dae_interpolation

出力ステップでの結果に対して積分器が補間を使用するかどうかを指定します。

TRUEは、ユーザーが要求した出力ポイントで、MotionSolveが（必要に応じて）結果を補間することを意味します。
FALSEは、ユーザーが要求した出力ポイントで、MotionSolveがDASPK積分器を使用して（必要に応じて）結果を補間することを意味します。

デフォルト = TRUE

積分器タイプがCSTIFFの場合は、この属性が無視されます。

数値的剛性と物理的剛性
数値的剛性は、“物理的”剛性とはかなり異なります。数値的剛性は、システムの減衰特性によって決まりますが、物理的特性は、システムに内在する剛性（システム内のスプリングなど）によって決まります。数値的剛性の概念は、作用点でのシステムの固有値に密接に関係しています。

システムの固有値には、実部と虚部の2つの成分があります。実部はシステムの減衰特性を定義し、虚部は作用点でのシステムの振動周波数を定義します。
- 虚部成分のない固有値は、過減衰振動モードを定義します。
- 実部成分のない固有値は、不減衰振動モードを定義します。
- 複素固有値は、不足減衰振動モードを定義します。
  数値的に硬いシステムは、次のプロパティを示す、非常に離れた固有値によって表現されます。
- 高周波成分は過減衰で、急速に減衰します。
- 解の低周波成分は不足減衰の挙動を示します。
  数値的剛性の概念は、以下に示す簡単な例を使用して説明されます。
  
  下の図は、2つの結合されていないスプリング質量システムを示しています。最初のシステムでは、質量M₁がプロパティK₁、C₁、およびL₀₁を持つスプリングで支持されています。2番目のシステムでは、質量M₂がプロパティK₂、C₂、およびL₀₂を持つスプリングで支持されています。全体座標系を基準にして測定された質量M₁の変位は、x₁と表されています。全体座標系を基準にして測定された質量M₂の変位は、x₂と表されています。
  以下を前提とします：
  - M1=1Kg、C1=2N sec/m、K1=10⁴ N/m
  - M2=1Kg、C2=2x104 N sec/m、K2=10⁸ N/m
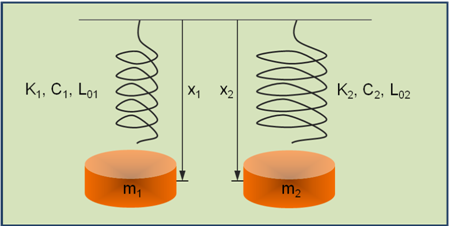
図 1. 結合されていない2つの単純なスプリング質量システム
各システムiにおいて、以下のことが容易にわかります：
- システムiの運動方程式：
  (1)
  $M_{i} {\ddot{x}}_{i} + C_{i} {\dot{x}}_{i} + K_{i} (x_{i} - L_{0 i}) = 0$
- システムiの固有値：
  (2)
  $λ_{i} = \frac{- C_{i} \pm \sqrt{C_{i}^{2} - 4 K_{i} M_{i}}}{2 M_{i}}$
- 最初のシステムの固有値と応答：
  (3)
  $\begin{array}{l} λ_{1} = - 1 \pm 99.995 i \\ x_{1} (t) = X_{01} e^{- (1 \pm 99.995 i) t} = X_{01} e^{- t} [\cos (99.995 t) + i \cdot \sin (99.995 t)] \end{array}$
- 2番目のシステムの固有値と応答：
  (4)
  
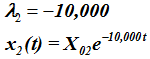
  システム1は不足減衰です。初期外乱に応じて振動の減衰が示されます。0.01秒後に、初期外乱は元の値のe^-0.01 = 0.99倍に減少します。システム1は、99.995ラジアン / 秒の周波数で振動します。
  
  一方、システム2は過減衰です。0.01秒後に、初期外乱は元の値のe^-100 = 3.72 x 10^-44倍に減少します。どのような初期外乱であっても、システム応答はほぼ瞬間的になくなります。システム2が振動することはありません。
  
  このような特性を表すシステムを数値的に硬いと言います。解のある成分が初期励起に対してゆっくりした減衰を示すのに対し、別の成分はほぼ瞬間的に消えます。
  
  多くの機構システムは、数値的に硬いプロパティを有しているか、微分代数方程式で表現されます（コメント2をご参照ください）。これらは、硬安定な積分器でのみ効果的に解析できます。
微分代数方程式
常微分方程式と代数拘束方程式を組み合わせた連立方程式は、微分代数方程式と呼ばれます。

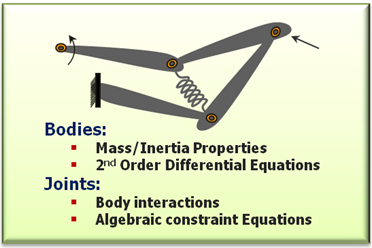
図 2. マルチボディシステム

例えば、マルチボディシステム（MBS）で、ニュートンの第二法則は2次の常微分方程式（ODE）で表され、このシステム内の拘束（ジョイントなど）は代数方程式（AE）で表されます。したがって、通常のマルチボディシステムの数式的表現は、連立微分代数方程式になります。上の図に示されたメカニズムは、通常、微分代数方程式で表現されます。

常微分方程式は次のように表されます：(5)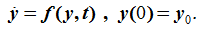

y は、積分される状態です。

微分代数方程式は次のように表されます：

(6)
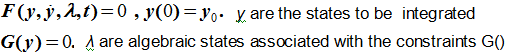
DAEのインデックス
連立DAEのインデックスは、連立常微分方程式を取得するために、独立変数（通常は時間）に関してシステム内の拘束を微分する回数として定義されます。これは、下の図に示すとおりです。

図 3. 連立DAEのインデックス
方程式定式化
MotionSolveは、動的シミュレーションの4種類の方程式定式化をサポートします。

ODE定式化

ODE定式化は、stiff積分器とnon-stiff積分器の両方をサポートします。MotionSolveは、coordinate partitioning法を用いてDAE形式の運動方程式をODE形式に変換し、そのうえで、ODE積分器を使って結果の方程式を解きます。stiff積分器とnon-stiff積分器の両方がサポートされています。この定式化によってサポートされるstiff積分器は、(a) VSTIFFと(b) MSTIFFです。non-stiffソリューションを積分するには、積分器ABAMが使用されます。

DAE Index-3 (I3)定式化

I3定式化は、DAE形式の運動方程式を、この形式の運動方程式を解くことのできる積分器に提供します。DSTIFFが、MotionSolveでI3形式の運動方程式を解くことのできる唯一の積分器です。I3定式化では、積分器は、速度の状態での積分のローカルエラーを監視しません。したがって、I3ソリューションは通常、非常に高速ですが、速度に関して多少正確さに欠ける傾向があります。

DAE Stabilized Index-1 (SI1)定式化

SI1定式化は、さらに“安定化させた”index-1 DAE形式の運動方程式を、この形式の運動方程式を解くことのできる積分器に提供します。“安定化させた”とは、I3セットに追加される速度と加速度の拘束の余剰と思われるセットに対して述べている言葉です。これらは、速度および加速度の、速度および加速度の拘束との一貫性を保ちます。解が正確であれば、これは自動的に行われます。DSTIFFが、MotionSolveでSI1形式の運動方程式を解くことのできる唯一の積分器です。SI1定式化では、積分器は、変位と速度の両方の状態での積分のローカルエラーを監視します。したがって、SI1ソリューションは通常、非常に正確であると言えます。SI2ソリューションのスピードはI3ソリューションのスピードに比較すると若干遅くなります。

上述したことをまとめると下の図のようになります。

図 4. MotionSolveでの積分器と方程式定式化
数値解法
MotionSolveは、動的シミュレーションの4種類の積分アルゴリズムを提供します。

DSTIFF

これは、MotionSolveのデフォルトの積分器です。このコードは、後退微分法（BDF）の組み合わせを使用して、G(t,y,y') = 0の形式の連立微分 / 代数方程式を解きます。これは、一般的に使用可能な積分器DASPKに基づいています。この積分器の作者は、Linda R. Petzold氏、Peter N. Brown氏、Alan C. Hindmarsh氏、およびClement W. Ulrich氏です。これは、ローレンスリバモア国立研究所（LLNL）、および後にカリフォルニア大学サンタバーバラ校で開発されました。この積分器は、MotionSolveでは、DAE形式の運動方程式（I3およびSI1）でのみ使用できます。

VSTIFF

これは、VODEに基づく、硬安定で、主係数が固定のBDF積分器です。VODEは、P.N.Brown（ローレンスリバモア国立研究所（LLNL））、G.D.Byrne（SMU）、およびA.C.Hindmarsh（LLNL）によって開発されました。これは、MotionSolveにおけるODE形式の運動方程式のデフォルトstiff積分器です。VODEは、dy/dt = f(t,y)の形式、またはdyi/dt =fi(t,y1,y2,...,yNEQ) (i = 1,...,NEQ)の成分形式の1次ODEの硬いまたは硬くないシステムの初期値問題を解きます。

VODE

EPISODEおよびEPISODEBパッケージと、ODEPACKユーザーインターフェース標準に基づき、小さな変更を加えたパッケージ。

MSTIFF

これは、J R Cashによって開発された、Modified Extended Backward Differentiation Formulae（MEBDF）に基づく、硬安定なBDF積分器です。この積分器は、MotionSolveでは、ODE形式の運動方程式でのみ使用できます。

ABAM (Adams-Bashforth-Adams-Moulton)

これは、Laurence F. ShampineとMarilyn K. Gordonによって作成された、non-stiff積分器です。この積分器は、MotionSolveでは、ODE形式の運動方程式でのみ使用できます。
Index-3 DAE形式の運動方程式
システムが次のように定義されているものとします：
- “N”個の変位座標q=[q1, q2, … qN]^Tを使用してシステムを表します。
- 座標qは、すべて独立しているわけではありません。
- “M”個の変位拘束Φ =[ Φ1(q,t), Φ2(q,t), … ΦM(q,t)]^Tが、“N”個の座標qの間に存在します。
- λ = [ λ1, λ2 … λM]^Tが、拘束Φを維持するために必要なLagrange乗数を表すとします。
- F = [F1, F2 … FNa]^Tが、システム上で作用する外力を表すとします。
- システムの運動エネルギーは、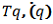、位置エネルギーは、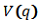とします。
- Lagrange関数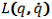は、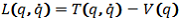と表されます。
  これらの仮定の下で、システムの運動方程式は次のように表現できます：
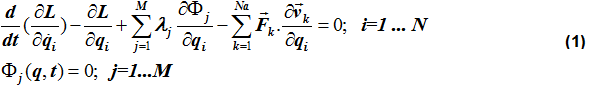
上記の方程式は、運動方程式のEuler-Lagrange表現と呼ばれます。マトリクス形式では、式（1）は次のように記述できます：

式（2.1）は、力の釣り合いの方程式を表します。最初の項は慣性力、2番目の項は拘束力、3番目の項は一般化外力を表します。式（2.1）は、したがって、ニュートンの運動の第二法則を書き換えたものとなります。式（2.1）は、速度（加速度）の時間導関数と、システムに作用する外力および内力を関連付ける微分方程式です。

式（2.2）は、システム内の運動微分方程式を表します。これらの式は、1次形式の運動方程式を表します。これを行うには、新しい一連の速度の変数uを作成します。速度は、変位の1次時間導関数として定義されます。式（2.2）も微分方程式です。

式（2.3）は、システム内の代数拘束を表します。これらが成立するのは、これらの方程式が、独立座標セットについて定式化されなかったためです。システムにはp=N-Mの自由度があります。したがって、N個の座標を、M個の代数拘束方程式により、互いに関連付けることができます。

式（2.4）は、Control_Diff、Control_SISO、およびControl_StateEqn要素を使用して指定される、ユーザー定義の微分方程式を表します。ユーザー定義の状態は、xで表されます。

式（2）は、一連の陰的な微分代数方程式（DAE）です。Z = [u, q, λ, x]^Tとします。式（2）は、圧縮表記で次のように表すことができます：

式（2.1）を1回、式（2.3）を3回微分することで、式（3）を次の形式の一連の常微分方程式（ODE）に変換することができます：

DAEのインデックスは、DAEを一連のODEに変換するために拘束を微分する回数として定義されます。式（4）で表されるODE形式に達するためには拘束（2.3）の3回微分が必要であるため、DAEのインデックスは3となります。Index-3 DAEは、以下のような特性もあります。

式（2）または（3）の数値解法には、専用のDAE積分器が必要です。これらの手法は、{u}、{q}、および{λ}の精度はさまざまなレベルに制御されるという基本概念を共有しています。一般的なアプローチの1つ（Index-3）が、{u}および{λ}での局所積分誤差を無視し、{q}での局所積分誤差のみを監視するというものです。したがって、Index-3の解法は精度は低下しますが、非常に高速になる傾向があります。非常に正確な解法が必要な場合には、代替アプローチが推奨されます。

硬安定な積分器を使用した運動方程式の数値積分

方程式の数値積分は選択した積分器で実行されます。現在、次の3つの硬安定な積分器が使用可能です：

VSTIFF、MSTIFF、およびDSTIFF
実行するには、積分器の選択に関係なく、主に次の3つの操作が必要です。

a）予測

予測子の目的は、修正子に優れた初期推測値を提供することです。予測子は、以前計算した解析ポイントを介して多項式をフィットさせます。その後、その多項式を時間の新しい値に外挿し、解を“予測”します。

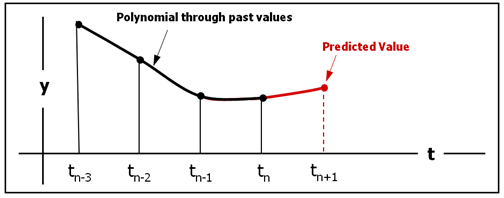
上の図は、DSTIFFの予測子の仕組みを示しています。T_nは現在の時間で、積分器はt_n+1の値を予測します。予測子の多項式は黒で示されています。外挿は赤レンガ色で示されています。予測子は単に過去の値を外挿するだけです。運動方程式を解くのではありません。積分器の次数は、使用する過去の値の数を定義します。図 5で、積分器の次数は3であるため、tnから初めて3つの過去の値が考慮されます。

DSTIFFはニュートン差分商を使用して補間多項式を作成します。この多項式の形式は次のとおりです：

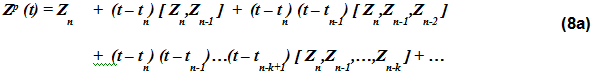
[ Z_n,Z_n-1 ]、[ Z_n,Z_n-1,Z_n-2 ]などの数量は、状態Z_nの差分商を表します。

VSTIFFおよびMSTIFFは、若干異なる方式を使用します。時刻tnにおいて次数Kの積分器は、K次の導関数を使用します。積分器は単に状態Zのテイラー級数展開を使用し、時刻t_n+1での解を予測します。これを次の式8に示します。

h = t_n+1 - t_n は、ステップサイズです。

b）修正

修正子の目的は、運動方程式を満たすよう、予測値を改善することです。

DAE-Index 3定式化の式（3）
stiffおよびnon-stiffの両方の積分器で修正子が使用されますが、それぞれで採用される手法は異なります。Index-3 DAE定式化の場合、DSTIFFは修正ニュートン-ラプソン（N-R）法を使用して、確実に解が運動方程式を満たすようにします。ニュートン-ラプソンの詳細については、DebugOutputの説明をご参照ください。この手法を採用するには、DAEを一連の非線形微分代数方程式に変換する必要があります。この変換について、以下に説明します。

stiff積分器の一般的な積分定式化は以下のとおりです：

式（9）において：

hは試みられるステップサイズ、kは積分器の次数です。
αj、β0は、積分器によって定義される係数です。これらは、使用される手法（VSTIFF、MSTIFF、またはDSTIFF）に依存します。
この積分定式化は、連立DAEを、N-R（修正子の最初フェーズ）が解くことのできる一連の非線形代数方程式（NLAE）に変換します。

修正子の目的をより正確に示すと、次のようになります：
予測子によって特定される予測値Z_n+1^(p)が与えられたら、運動方程式（式3または7）を満たす修正値Z_n+1^(c)を求めます。
予測値についてのG()の1次テイラー級数展開を使用して、以下の式が得られます。

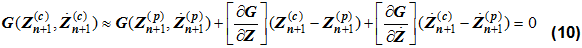
以下のように定義します：

次の式が成り立ちます：

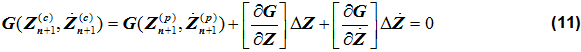
（9）より、次の式が得られます：

（12）を（11）に代入すると、修正子の関係が得られます：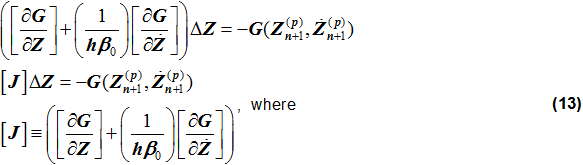

マトリクス[J]は、運動方程式のヤコビアンマトリクスと呼ばれます。（13）より、修正子の反復計算シーケンスは下の図に示すように定義されます。プロセスの中核には、非線形代数方程式を解くニュートン-ラプソン法があります。

下の図のように、DDWNRM(…)で誤差ノルムが計算されます。

上の図で：

RTOL[i]（相対トレランス）とATOL[i]（絶対トレランス）は、入力ファイルのPARAM_TRANSIENTブロックで指定される誤差トレランスINTEGR_TOLと、変数タイプに依存するスケールファクターから、次のように計算されます：RTOL[i] = ATOL[i] = INTEGR_TOL * SCALE[i]

SCALE[i]は、入力ファイルのPARAM_TRANSIENTブロックで指定される属性VEL_TOL_FACTORおよびDAE_ALG_TOL_FACTORから計算されます。詳細については次の表に示します。Zのさまざまな状態が次のようにスケーリングされます：

表 1. 解ベクトルのスケール値
状態タイプ	属性	スケールのデフォルト値
変位		1.0
微分状態		1.0
速度	`VEL_TOL_FACTOR`	1000.0
Lagrange乗数：	`DAE_ALG_TOL_FACTOR`	1000.0

変位およびユーザー定義の微分状態の場合：

RTOL[i] = ATOL[i] = INTEGR_TOL
速度状態の場合：
RTOL[i] = ATOL[i] = VEL_TOL_FACTOR*INTEGR_TOL
Lagrange乗数状態の場合：
RTOL[i] = ATOL[i] = DAE_ALG_TOL_FACTOR*INTEGR_TOL
c）局所切り捨て誤差の推定

修正子は、解が運動方程式（EOM）を満たしていること（EOMが一貫しているなど）は保証しますが、精度は保証しません。プロセスの次のステップでは、精度を推定するステップでの積分誤差の計算です。修正された解は“真の”解ではない可能性があるためです。むしろ、予測の精度が悪く、モデルの初期条件に一致しなくなっている解を修正子が見つけることもあります。言い換えれば、結果は、EOMとは一致しないが、解多様体の別の解に“行きついた”可能性があるということです。誤差の計算を次の図に示します。Ckは、積分器によって計算されるステップサイズの誤差係数です。

減衰の大きい問題に対してstiff積分器が有効なのはなぜでしょうか？
これを理解するには、次のテスト問題を考えてみます：

この問題の真の解は次のとおりです：

後退オイラー法は、1次のstiff積分器です。次の形式を取ります：

（16）を式（14）に適用すると、以下が得られます：

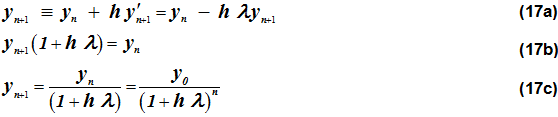
hの任意の正の値について、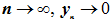となります。後退オイラー法は、hのどの値に対しても安定しています。ステップサイズhが大きいと、y_n+1はより速くゼロに収束します。

これに対し、前進オイラー法の積分器（1次のnon-stiff積分器）で同じ計算を行うと、次のような結果となります。前進オイラー法の形式は次のとおりです：

（18）を式（14）に適用すると、以下が得られます：

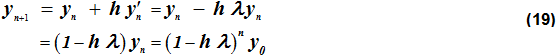
式（19）は、前進オイラー法について、次のとおりであることを示しています：

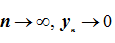、ただし、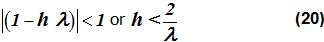

式（14）でl=10⁴という大きな減衰が生じる問題について考えます。
- 式（20）は、前進オイラー法では、ステップサイズがh < 2 x 10^-4の場合にのみ、安定した結果が得られることを示しています。
- 式（17c）は、後退オイラー法では、任意のステップhに対して、安定した結果が得られることを示しています。
  これは、stiff積分器が減衰の伴う問題に非常に効果的であるためです。
積分器の失敗によりモデルが失敗します。この問題をどのように診断し、修正することができるでしょうか？
DSTIFFやVSTIFFなどのマルチステップ積分器は、各ステップで、解の予測値と修正された値の差を計算し、積分器で計算される“誤差係数”でそれをスケーリングすることで、局所的な誤差を推定します。したがって、不適切な予測により、積分誤差が生じる可能性があります。
予測が不正確になる理由として次の2つが考えられます：
- システム内に不連続なモーション入力がある。
- システム内にほぼ不連続な力がある。
  下の図10aおよび10bに、このようなモデル化の影響を示します。
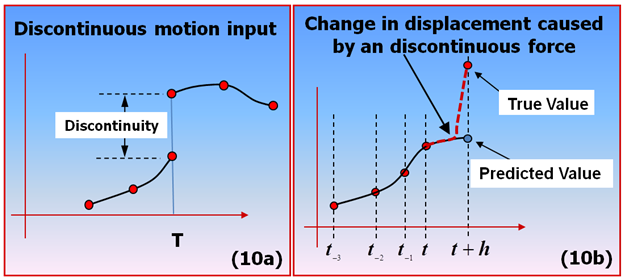
図 9. 不連続性が積分の失敗の根本原因
上記のような不連続性は、IF-THEN-ELSEロジックを不用意に使用した関数表現やユーザーサブルーチンによって生じることがあります。不連続性や急な変化がないかを調べる必要のあるモデリング要素には、次のようなものがあります：
- Forces
- 変数
- ユーザーの微分方程式
- 一般状態方程式
  IF-THEN-ELSEロジックを滑らかなSTEP関数に置き換えることをお勧めします。また、MotionSolveのXMLステートメント：
```
<DebugOutput>
      SwitchOn="True"
</DebugOutput>
```
  を使用して、詳細なニュートン-ラプソン反復の出力を有効にしてください。この出力を確認することで、通常は失敗の原因になりそうなモデリング要素まで戻ることができます。
  
  このような状況での通常の修正は、次のとおりです：
- 剛性 / 減衰係数が現実的であることを確認する。
- 質量および慣性が物理的に意味のあるものであることを確認する。
- モデリング要素内の不連続性を特定し、排除する。
- 非常に急なSTEP関数を避ける。
- 真の原因を把握するため、一時的にINTEGR_TOLを緩和する。
結果は収束していますか？つまり、誤差トレランスと共に変化しなくなりましたか？
収束スタディを実施して、積分器から取得した結果が変化しなくなっている（収束している）ことを確認することをお勧めします。積分器は正確な解を近似するため、積分器内で許容される誤差が多すぎる場合、誤差トレランスが厳しい（小さい）場合とは異なる結果を積分器が提供することがあり得ます。必要に応じて積分器を調整できるようにする設定はある程度ありますが、最初に調査を開始するために使用できるいくつかの設定を以下に示します：
- integr_tol
- h_max
- （DSTIFF用のvel_tol_factor。これには、dae_indexパラメータを経由してSI1が必要です）。
収束した結果はさまざまな方法で取得できますが、ユーザーに有効な一例を以下に示します：
- モデル内の注目するデータのチャネルを選択します（変位、力など）。
- 積分器を選択します。 - その積分器で何の誤差制御を行いますか？（変位、速度、微分状態）
- 積分器が収束を制御する状態まで、誤差を低減します。収束結果を得ることができる最大誤差を取得します。
- まだ積分器が誤差トレランスを使用して制御できない状態に注目している場合は、そのような状態が収束するまで積分器の最大ステップサイズ（h_max）を下げ、収束結果を得ることができる最大のh_maxを使用します。
- シミュレーションが失敗した場合、誤差トレランスを緩和（大きく）して積分器の最大ステップサイズ（h_max）の精度を制御し、問題のシミュレーションを成功させます。これは可変ステップの積分器より時間がかかるため、最後の手段として使用します。
- その他多くの積分器設定も使用可能です。自分のモデルに適用できるその他のオプションも使用してみてください。

さまざまな定式化アプローチの相対比較

以下の表は、さまざまなDAEアプローチの相対的な利点をまとめたものです。さまざまなアプローチを特徴付けるにあたり、次の基準を使用しています：

精度

解の配列で累積される積分誤差（図図 5で計算されたもの）を測定します。

速度

さまざまなアプローチで共通する相対CPU時間を測定します。これはモデルに大きく依存し、さまざまなアプローチをテストする際のデータに対する経験が反映されます。

不連続性の処理

定式化がシステム入力（モーションまたは力）の尖った角や不連続性を処理する能力を測定します。不連続性や尖った角（非微分可能性）は、モデルで回避する必要があります。

一貫性: 解が拘束Φ、その1次および2次時間導関数をいかに満たしているかを測定します。
高周波の追跡: システム内の高周波がいかに追跡されているかを測定します。
数値減衰: 特定のインデックス定式化の実装により適用された数値減衰を測定します。一般に、数値減衰が大きい場合、精度は低下しますが、高速でより堅牢な解が得られます。
堅牢性: デフォルトのDE定式化はIndex-3です。最初にIndex-3定式化を使用し、上記の基準を満たさない解が見つかった場合にのみ別の定式化への切り替えを検討することをお勧めします。

注: 次の表は、主観的な情報を含んでおり、絶対的な推奨事項ではなく、一般的なガイドラインとして使用してください。

表 2. さまざまな方程式定式化の相対的な利点
	I-3	SI-1	ODE (SI-0)	ABAM
精度	中	高	高	高
速度	高	中	低	高 / 非常に低い＊
不連続性の処理	高	低	低	高
一貫性	低	高	高	高
高周波の追跡	低	高	高	高
数値減衰	高	低	低	低
堅牢性	高	中	中	高

（＊ABAMの場合、硬くない問題に対しては高速、硬い問題に対しては非常に低速になります。）

DAE_CONSTR_TOLを0.001mmより大きな値にすることは、ほとんどの場合お勧めしません。このトレランスが、モデルの長さ単位で指定されたシステム内の運動拘束の最低限の解析精度となります。DAE_CONSTR_TOLが大きい（0.001mmより大きい）場合、システム拘束は緩く満たされるだけになります。不正確な応答が作成されるだけでなく、拘束充足における誤差により数値的な解が不安点になり、失敗につながることもあります。

dae_jacob_evalとdae_jacob_init はどちらも、修正子の反復計算時にヤコビアンを評価するタイミングを制御します。この2つの主な違いは、ヤコビアン評価の頻度に影響を与える方法です。

Mをニュートン-ラプソン反復の反復カウンターとします。このインデックスが0インデックスとして実装されていることに注意してください。これは0から開始することを意味します。ヤコビアンは、次の条件のいずれかまたは両方が満たされるたびに再評価されます。

MOD(M, dae_jacob_eval) = 0
M < dae_jacob_init

これを以下の表にわかりやすく示します。

修正子反復カウンター（M）	dae_jacob_eval = 2	dae_jacob_init = 2	新しいヤコビアン？
修正子反復カウンター（M）	MOD (M, 2) = 0?	M < 2?	新しいヤコビアン？
0	○	○	○
1	×	○	○
2	○	×	○
3	×	×	×
4	○	×	○

修正子反復カウンター（M）	dae_jacob_eval = 3	dae_jacob_init = 2	新しいヤコビアン？
修正子反復カウンター（M）	MOD (M, 3) = 0?	M < 2?	新しいヤコビアン？
0	○	○	○
1	×	○	○
2	×	×	×
3	○	×	○
4	×	×	×
5	×	×	×
6	○	×	○
7	×	×	×

参考資料
VSTIFF:
- “VODE, a Variable-Coefficient ODE Solver”、P. N. Brown、G. D. Byrne、およびA. C. Hindmarsh、SIAM J. Sci.Stat.Comput.、10、1038-1051ページ、1989年。
- “A Poly-algorithm for the Numerical Solution of Ordinary Differential Equations”、G. D. ByrneおよびA. C. Hindmarsh、ACM Trans.Math.Software、1（1975年）、71-96ページ。
- “EPISODE: An Effective Package for the Integration of Systems of Ordinary Differential Equations”、A. C. HindmarshおよびG. D. Byrne、LLNL Report UCID-30112、Rev. 1、1977年4月。
- Scientific Computingの“ODEPACK, a Systematized Collection of ODE Solvers”、 A. C. Hindmarsh、R. S. Stepleman他（編）、North-Holland、Amsterdam、1983年、55-64ページ。
DSTIFF:
- “The Numerical Solution of Initial Value Problems in Differential-Algebraic Equations”、L. Petzold、K. E. Brenan、およびS. L. Campbell、Elsevier Science Publishing Co.、（1989年）、2版、SIAM Classics Series、1996年。
- “Consistent Initial Condition Calculation for Differential-Algebraic Systems”、P. N. Brown、A. C. Hindmarsh、およびL. R. Petzold、SIAM J. Sci.Comp.19（1998年）、1495-1512ページ。
MSTIFF:
- “The Integration Of Stiff Initial Value Problems In O.D.E.S Using Modified Extended Backward Differentiation Formulae”、J. Cash、Comp. and Maths. with Applics.、9:645-657、1983年。
- “The Integration Of Stiff Initial Value Problems In O.D.E.S Using Modified Extended Backward Differentiation Formulae”、J.R.Cash、Comp.And Maths.With Applics.、9、645-657、（1983年）。
- “Stable Recursions With Applications To The Numerical Solution Of Stiff Systems”、J.R.Cash、Academic Press、（1979年）。
- “Ordinary Differential Equation System Solver”、A.C.Hindmarsh、Gear, C.W.、Ucid-30001 Rev. 3、Lawrence Livermore Laboratory、Livermore、Ca 94550、1974年12月。
- “An Mebdf Code For Stiff Initial Value Problems”、J.R.CashおよびS. Considine、ACM Transactions On Mathematical Software、1992年。
  ABAM:
- “Computer Solution of Ordinary Differential Equations”、Lawrence F. ShampineおよびMarilyn K. Gordon、W.H.Freeman & Co Ltd、1975年6月。