OS-V: 0080 Buckling of Shells and Composites with Offset
A test of influence of offset on buckling solution for shells, including composite with offset Z0 and element offset ZOFFS.

図 1. FE Model of the Beam with Boundary Conditions and Loadcases
Benchmark Model
Here, you solve several problems to calculate the critical load on different conditions. The model is a simply supported beam of height 1mm, breadth 2mm and length 100mm with one end constrained in all DOFs and an axial load applied on the other end.
- MAT1
- Young's Modulus
- 1 x 106 N/mm2
- Poisson's Ratio
- 0.0
- Density
- 2 kg/mm3
- Thermal Expansion Coefficient
- 1 x 10-4 ºC-1
- Reference Temperature for Thermal Loading
- 300ºC
- Buckling without offset.
- Buckling with moment equivalent to offset.
- Buckling with offset created by a frame.
- Buckling with offset applied through ZOFFS.
- Buckling of composite with non-symmetrical layup.
- Buckling of composite with offset.
- Maximum or critical force
- Modulus of elasticity
- Area moment of inertia (second moment of area)
- Unsupported length of the beam
- Column effective length factor (for one end fixed and the other end free, =2)
Results

図 2. First Four Buckling Eigenvalues for Non-offset (z0 = -0.5)
| Quantity | Theoretical | No-offset | Normalized |
|---|---|---|---|
| cr(1) | 4.1123 | 4.1208 | 0.997937 |
| cr(2) | 16.449 | 16.513 | 0.996124 |
| cr(3) | 37.011 | 37.701 | 0.981698 |
| cr(4) | 102.81 | 108.19 | 0.950273 |

図 3. First Four Buckling Eigenvalues for Non-offset + Moment . (the effect of offset is simulated by adding a moment at the end of the beam)
| Quantity | Theoretical | No-offset + Moment | Normalized |
|---|---|---|---|
| cr(1) | 4.1123 | 4.1208 | 0.997937 |
| cr(2) | 16.449 | 16.513 | 0.996124 |
| cr(3) | 37.011 | 37.701 | 0.981698 |
| cr(4) | 102.81 | 108.19 | 0.950273 |

図 4. First Four Buckling Eigenvalues for C-Frame. (the effect of offset is simulated by creating a C-shaped frame)
| Quantity | Theoretical | C-Frame | Normalized |
|---|---|---|---|
| cr(1) | 4.1123 | 4.1208 | 0.997937 |
| cr(2) | 16.449 | 16.513 | 0.996124 |
| cr (3) | 37.011 | 37.700 | 0.981724 |
| cr(4) | 102.81 | 108.19 | 0.950273 |

図 5. First Four Buckling Eigenvalues for z-offset (Zoffs = -0.5)
| Quantity | Theoretical | ZOFFS | Normalized |
|---|---|---|---|
| cr(1) | 4.1123 | 4.1208 | 0.997937 |
| cr(2) | 16.449 | 16.513 | 0.996124 |
| cr(3) | 37.011 | 37.700 | 0.981724 |
| cr(4) | 102.81 | 108.19 | 0.950273 |
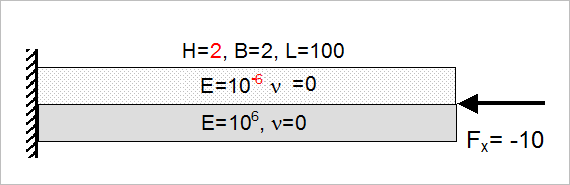
図 6. First Four Buckling Eigenvalues for Non-symmetric Layup . (since the top layer is very weak, the load is applied to the “strong” layer with an offset of 0.5)
| Quantity | Theoretical | Non-symmetric Layup | Normalized |
|---|---|---|---|
| cr(1) | 4.1123 | 4.1203 | 0.998058 |
| cr(2) | 16.449 | 16.510 | 0.996305 |
| cr(3) | 37.011 | 37.663 | 0.982689 |
| cr(4) | 102.81 | 107.89 | 0.952915 |

図 7. First Four Buckling Eigenvalues for Composites with Offset (z0 = -1)
| Quantity | Theoretical | Offset Composite | Normalized |
|---|---|---|---|
| cr(1) | 4.1123 | 4.1203 | 0.998058 |
| cr(2) | 16.449 | 16.510 | 0.996305 |
| cr(3) | 37.011 | 37.663 | 0.982689 |
| cr(4) | 102.81 | 107.89 | 0.952915 |
Model Files
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
The model files used in this problem include:
- s100comp_buckl.fem
- s100compmom_buckl.fem
- s100comp_frame_buckl.fem
- s100comp_buckl_zoffs.fem
- s100comp2ply_buckl.fem
- s100compoffs_buckl.fem