フリー寸法最適化
フリー寸法最適化は、HyperMeshのOptimization panelでサポートされているDSIZEバルクデータエントリで定義されます。
フリー寸法最適化で使用可能なフィーチャーには、最小部材寸法の制御、対称面、パターングルーピングとパターン繰り返し、および、構造全体のフォンミーゼス応力への応力制約条件の適用が含まれます。
同じ最適化問題にトポロジー最適化とフリー寸法最適化を両方適用することは推奨されません。これは、トポロジーコンポーネント上のペナルティが偏りを生み、最適状態には及ばない解を導く結果となり得るためです。
問題の定式化
シェル断面(下の図参照)については、フリー寸法最適化では、各要素の板厚tをTとT0の間で自由に変化させることができます。これは、TまたはT0のいずれかの離散板厚をターゲットとするトポロジー最適化と対照をなします。

図 1. シェル断面
例:片持ち梁プレート
片持ち梁プレートを下の図に示します。ベース-プレート板厚T0はゼロです。最適化問題の設定は次の通りです:
コンプライアンスの最小化

図 2. 片持ち梁プレート
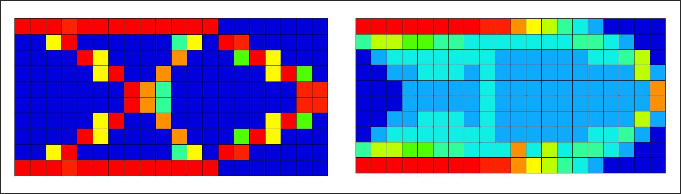
図 3. トポロジー結果(左); フリー寸法結果(右)
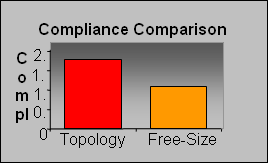
図 4.
コンプライアンスに関してはフリー寸法設計のほうがトポロジー設計より優れていることに別に不思議はありません。これは、連続した板厚の変化はより大きな設計の自由度を提供するためです。
図 5. 片持ち梁プレート – 3次元モデル
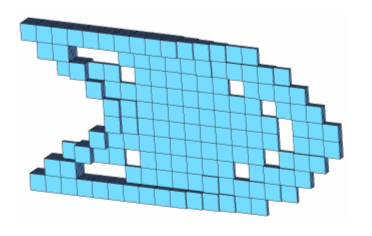
図 6. 3次元トポロジー結果
上の図の3次元モデルのトポロジー設計は、先に示したフリー寸法最適化結果と似ているように見えます。これは驚くべきことではありません。なぜならば、プレートが3次元でモデル化される際、各要素について0または1の離散密度値を求めるトポロジー定式化では、変化する板厚分布は可能となります。非常に精細な3次元要素が使用される場合、プレートの連続的に変化する板厚は、トポロジー最適化によって求めることができます。フリー寸法最適化導入の動機は、2次元モデル化による制限が最適化の定式化の障害となってはならないという考えに基づいています。シェルの3次元モデル化に関しては、トポロジー最適化は、3次元モデル化されたシェルの板厚方向への押し出し制約条件の適用と同じです。
フリー寸法設計は広範囲にわたる空洞なしに板厚が変化するシェルを作成することが多い一方、最適化エンジンがそれを要求する場合は空洞を抑制しない点に注意することが大切です。先に示した例では、45度領域、サポートに隣接の箇所、およびフリーエンドの上下角部分に空洞が認められます。
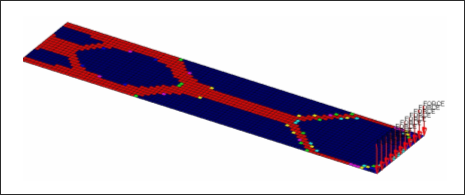
図 7. 曲げを受けるプレートのフリー寸法結果
トポロジー最適化およびフリー寸法最適化の応力応答
トポロジー最適化およびフリー寸法最適化の実際の応力応答は、DRESP1バルクデータエントリ上の対応する応力応答RTYPEを通して得られます。Stress-NORMの集計は、モデル内の要素のグループについて応力応答を計算するために使用されます。
トポロジー最適化またはフリー寸法最適化におけるフォンミーゼス応力
- 応力の制約条件は、1つのフォンミーゼス許容応力に限定されます。異なる許容応力を有する異なる材料が構造内に存在する場合、特異トポロジーの現象が発生します。特異トポロジーは、応力の制約条件の条件付き性質に関連した問題のことで、要素がなくなると、要素の応力制約条件は消失します。これは、設計スペース全体で勾配ベースの最適化エンジンによって通常解くことができないほど多数の縮退問題が存在してしまうという別の問題を生じます。
- 部分領域の削除によりすべての応力制約条件が削除される惧れがあり、これにより最適化問題が正しく設定されなくなるため、構造の部分領域についての応力の制約条件は許可されません。したがって、応力の制約条件は、アクティブである際は、設計領域と非設計領域の両方を含むモデル全体に適用され、応力制約条件の設定は、すべてのDSIZEおよびDTPLカードについて等しくなければなりません。
- 集中荷重および集中境界条件によって生じる人工的応力制約条件をフィルタにかけるために、ビルトインインテリジェンスが装備されています。境界形状に起因する応力集中も、局所的な形状の最適化でより効率的に改良されるよう、ある程度フィルタにかけられます。
- 応力の制約条件がアクティブである要素が多数あるために、.outファイル内の保持された制約条件の表に要素応力のレポートが示されません。モデルの応力の状態の反復計算履歴は、HyperViewまたはHyperMeshで確認できます。
- 応力の制約条件は、1次元要素には適用されません。
- モデル内に強制変位が存在する場合、応力の制約条件は使用されない場合があります。
トポロジーおよびフリー寸法の設計特性の比較
トポロジーとフリー寸法の特性の違いを以下にリストします。座屈制約条件が無視される際は、フリー寸法設計概念は一般的により良いパフォーマンスを達成しますが、寸法最適化または形状最適化もしくはその両方のステージで座屈制約条件が推進条件となる場合、トポロジー概念はフリー寸法を凌ぐことがあります。これは、トポロジー最適化は中間板厚を排除し、そのため、面外の座屈に対してより強いシェルとより集中した材料分布が生じるためです。トポロジー最適化とフリー寸法最適化のパフォーマンスは、次の例で比較されます。与えられた構造についてどの条件が最もクリティカルであるかを知ることは通常不可能であるため、詳細の寸法および形状最適化が完了し、評価できるまで、両方の設計概念をフォローすることが推奨されます。各構造コンポーネントについて2つの設計を求めることができない場合は、共通して評価される構造の各タイプについて両方の概念の相対パフォーマンスのベンチマーク評価を行い、一般的なガイドラインが参照用に使用できるようにします。
- 例えば、標準のシートメタルを用いて製造される自動車のシェル構造のほとんどがそうであるように、変化する板厚シェルを製造するのは高価過ぎて実行可能な選択肢ではない場合。
- 構造の機能が設計内に広範に及ぶ空洞を必要とする場合。例えば、ケーブル、パイプ、その他の機器等を通すために大きな空洞が必要な、梁を支える航空機胴体フロアなど。
| シェルトポロジー最適化 | フリー寸法最適化 |
|---|---|
| 目的: 0/1板厚 自由度を制限 |
目的: 変数板厚 上限T以下で"自由」 |
| 結果: トラス状の設計概念 | どちらかといえば、面内荷重については変化する板厚パネル、曲げが主である場合は0/1板厚 |
| 非常に精細な3次元要素でシェルがモデル化されている場合、押し出し制約条件と同等 | 非常に精細な3次元要素によるモデルと同等 |
| フリー寸法と比べて役に立たない? | 常により優れた設計か? |
| 製造用制約条件 - 一定板厚の穿孔シートメタル | 製造 - 高価であり、コストに敏感でない業界のみで使用 |
| 集中全板厚部材は面外座屈に対してより強固 | 広幅の薄肉シェルは座屈しやすい |
| 他の非構造コンポーネント用、またはラインやパイプを通すために穴が必要とされる場合がある | 空洞は最適性によってコントロールされ、面内荷重下においては通常広範ではない |
フリー寸法結果の解釈
ほとんどの場合、シェル構造の変化する板厚は、階段状に求められます。フリー寸法結果は、板厚の異なる領域がどのように設計されるべきかの異なる概念を提供します。
その上で、詳細な寸法最適化を実行し、最終設計を微調整します。このプロセスを例:航空機のドア構造の梁をサポートで示します。
例:航空機のドア構造の梁をサポート
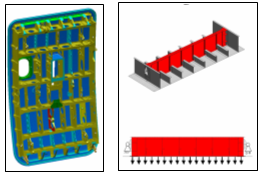
図 8. 航空機のドア構造の梁をサポート
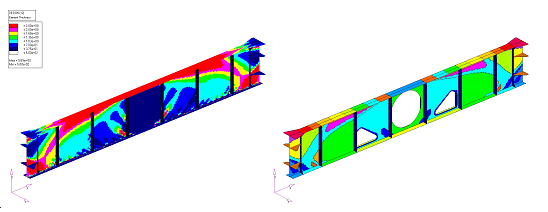
図 9. フリー寸法の結果(左); 変換処理された一定板厚の領域(右)
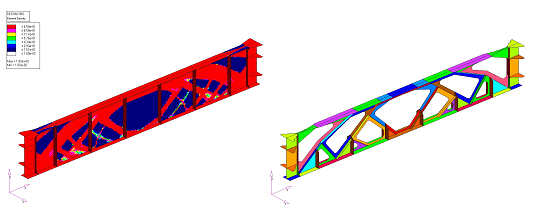
図 10. トポロジーの結果(左); 変換処理された一定板厚の領域(右)
- 梁の最大変形< 3.0 mm
- 梁設計領域内の最大フォンミーゼス応力< 300 MPa
- 座屈荷重係数 > 1.0

図 11. 異なる変形制約条件についての結果の比較