勾配ベースの最適化手法

本セクションでは、下記の各項について説明しています：

反復ソリューション

OptiStructでは局所近似法と呼ばれる反復手順を使用し、以下の手順で最適化問題の解を求めます。

有限要素を使用した物理的な問題の解析。
収束に至ったかどうかの収束テスト
現在の反復について潜在的にアクティブな応答を保持するための応答のスクリーニング
保持された応答についての設計感度解析
感度情報を使用して作成された近似問題の最適化。1.に戻る

安定した収束を得るため、各反復計算中の設計変数の変化は、境界内の狭い範囲に制限されています（ムーブリミットと呼ばれる）。最初のいくつかの反復計算中に発生する大きな設計変数の変化、および、高度な定式化やその他の安定化の手法のため、実際の収束は、ごくわずかな回数のFE解析のみで達成されます。

設計感度解析は、設計変数に対する構造応答の導関数を計算します。これは、シンプルな設計検証ツールや自動化された設計最適化フレームワークにとって、FEAの実施によって得られる最も重要な要素です。

設計の変更は、感度情報に基づいた近似最適化問題を解くことで生成されます。OptiStructは、双対法と可能方向法の２種類の最適化手法を備えています。双対法は、アクティブな制約条件に関連したラグランジュ乗数の双対空間で最適化問題を解きます。設計変数が非常に数多く、制約条件は少ないような設計問題（トポロジーおよびトポグラフィー最適化では一般的）には極めて効率的です。可能方向法は、元の設計変数空間で最適解を求めます。設計の制約条件と設計変数が同数程度である問題（寸法最適化や形状最適化では一般的）に使用されます。最適化手法の選択は、最適化問題の特徴に基づいてOptiStructによって自動的に行われます。

通常の収束と緩い収束

OptiStructでは２つの収束テストが使用され、そのいずれかを満足する必要があります。

２回の連続する反復計算で収束基準が満たされると、通常の収束が得られます（設計が可能）。これは、２回の連続する反復計算において、目的関数の変化がそのトレランス未満で、制約条件の違反が1%未満であることを意味します。収束は真の目的関数の値（最新の設計ポイントにおける解析から得られる値）の比較に基づくため、通常の収束には3回以上の解析が必要です。例外（設計が不可能）は、制約条件の違反が1%以上、および、３回の連続する反復計算において目的関数の変化がトレランス未満で制約条件の違反の変化が0.2%未満の際です。この場合、反復プロセスは、‘可能な設計が得られない’という結論で終了します。

２回の連続する反復計算の設計変数に変化がほとんどない、または変化がないと、緩い収束が得られます。前の反復計算からモデルが変化していないので、最終の設計ポイントについて目的関数（または制約条件）を評価する必要はありません。したがって、緩い収束に必要な反復計算は、通常の収束より1回少なくてすみます。

最適化アルゴリズム

OptiStructでは、勾配ベースの最適化アルゴリズムを使用して、最適化問題を解きます。

OptiStructでは次のアルゴリズムを使用できます：

可能方向法（MFD）
逐次2次計画法（SQP）
分離可能な凸近似に基づく2重最適化（DUAL）
分離可能な凸近似に基づく拡張2重最適化（DUAL2）
大規模最適化アルゴリズム（BIGOPT）
Method of Moving Asymptotes（MMA）

MFD、SQP、DUAL、DUAL2は標準の最適化アルゴリズムです。詳細については、参考文献セクションの関連資料をご参照ください。BIGOPTの詳細については、後続のセクションをご参照ください。

実行中に、OptiStructにより最適化タイプに基づいて対応する最適化アルゴリズムが自動的に選択されます。DOPTPRM, OPTMETHパラメータは、デフォルトの最適化アルゴリズムを変更するために使用することができます。このパラメータを使用すると、デフォルトが無効になります。

DUAL2は、独自のCONLIN2重最適化エンジンの拡張バージョンです。ソリューションの安定性が向上して、解が収束する際に不具合が発生する確率が低減されています。トポロジー、フリー寸法、トポグラフィーなど、設計変数が多い問題でデフォルトで使用される最適化エンジンは、DUAL2です。デフォルトのDUAL2法がトポロジー、フリー寸法、またはトポグラフィー最適化で収束しない問題に遭遇した場合には、DUALまたはMMAに切り替えることができます。

MFDは、拘束が多いものの設計変数が少ない問題（寸法 / ゲージや形状など）でデフォルトで使用する最適化エンジンです。

寸法 / ゲージや形状にはMFD、SQP（主要な方法）、およびBIGOPTがより適しています。これは近似の問題では一般的に、中間変数と応答を用いた進んだ近似定式化による連成項を含むからです。

寸法と形状の最適化で等式の制約条件がアクティブになっている場合は、SQPがデフォルト最適化エンジンです。

DOPTPRM,OPTIMOMP,YESは、MFD、SQPおよびDUAL2アルゴリズムについて並列計算をオンにするために使用できます。

大規模最適化アルゴリズム（BIGOPT）

勾配ベースの手法は、MFDやSQPと比べると、メモリ消費量が少なく、より効率的に計算できます。

インプリメンテーション

一連の制約に基づいて、

f (x)

を最小化する必要がある最適化問題を考えてみます。これは次のように表されます：(1)

\begin{array}{l} \min [f (x)] \\ g_{i} (x) = 0, i = 1, ..., m_{e} \\ g_{i} (x) \leq 0, i = (m_{e} + 1), ..., m_{e} \\ x^{L} \leq x \leq x^{U} \end{array}

ここで、 $f (x)$ は目的関数、 $g_{i} (x)$ はi番目の制約条件、 $m_{e}$ は等式の制約条件の数、 $m$ は制約条件の合計数、 $x$ は設計変数のベクトル、 $x^{L}$ と $x^{U}$ はそれぞれ設計変数の下限ベクトルと上限ベクトルです。

BIGOPTを選択すると、OptiStructはペナルティ法を使用して、この問題を次のように等価問題に変換します：(2)

\begin{array}{l} \min Φ (x) = f (x) + r (\sum_{i = 1}^{m_{e}} q_{i} {[g_{i} (x)]}^{2} + \sum_{i = m_{e} + 1}^{m} q_{i} {m a x [0, g_{i} (x)]}^{2}) \\ x^{L} \leq x \leq x^{U} \end{array}

ここで、 $r$ と $q_{i}$ はペナルティ乗数です。

BIGOPTでは上限制約条件と下限制約条件を分けて考えます。このため、元の問題が制約されていない問題に変換されます。探索の方向を生成するには、Polak-Ribiere共役勾配法を使用します。探索の方向が計算されたら、放物線補間によって1次元探索が実行されます（Brentの手法）。

終了の条件

BIGOPTアルゴリズムに基づく最適化の実行は、次のいずれかの条件が満たされた場合に終了します。

$‖ \nabla Φ ‖ \leq ε$ で、設計が可能。
$\frac{2 | Φ (x^{k + 1}) - Φ (x^{k}) |}{| Φ (x^{k + 1}) | + | Φ (x^{k}) |} \leq ε$ で、設計が可能。
反復ステップ数が $N_{\max}$ を超えた。

ここで、 $\nabla Φ$ は $Φ (x)$ の勾配、 $k$ は $k$ 番目の反復ステップ、 $εε$ は収束パラメータ、 $N_{\max}$ は許容される最大反復数です。

感度解析

応答量

g

は、変位から次のように計算されます：(3)

g = q^{T} u

設計変数

x

に関するこの応答の感度、すなわち応答の勾配は次のようになります：(4)

\frac{\partial g}{\partial x} = \frac{\partial q^{T}}{\partial x} u + q^{T} \frac{\partial u}{\partial x}

感度解析へのアプローチとして、直接法と随伴変数法が可能です。運動方程式は次のように与えられます。(5)

K u = f

設計変数

x

に関して微分すると、(6)

\frac{\partial K}{\partial x} u + K \frac{\partial u}{\partial x} = \frac{\partial f}{\partial x}

変位ベクトル

u

の感度は次のように計算できます：(7)

K \frac{\partial u}{\partial x} = \frac{\partial f}{\partial x} - \frac{\partial K}{\partial x} u

この式を使用した応答勾配の計算で最も手間がかかる処理は、設計変数に対する変位ベクトルの導関数の計算に必要な前進消去-後退代入です。これは直接法と呼ばれます。各設計変数につき、前進消去-後退代入が1回必要です。

複数の荷重のケースで制約条件がアクティブになっており、荷重が設計変数の関数（たとえば、形状最適化のための物体力または圧力荷重）である場合、アクティブな荷重のケースごとに、前進消去-後退代入のセットを実行する必要があります。荷重が設計変数の関数になっていなくても、複数の境界条件のあるアクティブな荷重ケースがある場合、アクティブな境界条件ごとに前進消去-後退代入を行う必要があります。

感度解析の随伴変数法では、ベクトル（随伴変数）

a

が導入され、次のように計算されます：(8)

K a = q

すると、制約条件の導関数は、次のように計算できます。(9)

\frac{\partial g}{\partial x} = \frac{\partial q^{T}}{\partial x} u + a^{T} (\frac{\partial f}{\partial x} - \frac{\partial K}{\partial x} u)

感度解析に随伴変数法を使用する場合、保持された制約条件ごとに前進消去-後退代入が１回必要となります。この前進消去-後退代入は、ベクトル $a$ を計算するために必要です。

一般的に形状およびサイズの最適化では、設計変数は少なく（たとえば5～50個）、制約条件は多くなります。多くの制約条件は応力の制約条件に由来します。応力の制約条件を1つずつ持つ20,000の要素と、10の荷重ケースがある場合、合計で200,000の応力の制約条件が見込まれます。

一般的にトポロジー最適化の設計変数は多く（各要素につき1～3）、制約条件は少なくなります。通常、トポロジー最適化では応力の制約条件は考慮されないので、演算上の負荷を軽減する目的で、感度解析の随伴変数法をトポロジー最適化に使用することには意味があります。

形状および寸法（パラメータ）の最適化では、感度解析に直接法を使用すると効果的なことがよくあります。ただし、設計変数が多く、制約条件が少ない場合は、随伴変数法を使用します。たとえば、トポグラフィー最適化では、制約条件をスクリーニングすることで、勾配の計算に必要な制約条件の数を削減できます。制約条件のスクリーニングにより、違反の可能性が低い制約条件は無視されます。違反している制約条件、またはほぼ違反している制約条件のみが考慮されます。また、応力集中のように構造の小さな領域に保持されている応力の制約条件が多数ある場合は、最も重要ないくつかの制約条件のみを考慮するだけですみます。

設計変数に関する応答の感度は、Excelスプレッドシートにエクスポート（OUTPUT, MSSENS）、もしくはHyperGraphでプロット（OUTPUT, HGSENS）することが可能です。HyperViewでコンター表示するために、トポロジー、フリー寸法、およびゲージの設計変数の感度をH3Dフォーマットにエクスポートすることが可能です（それぞれOUTPUT, H3DTOPOLおよびOUTPUT, H3DGAUGE）。トポロジーおよびフリー寸法変数についてのASCIIフォーマットの感度出力は、OUTPUT,ASCSENSSを介して要求できます。

DOPTPRM,DESMAX,0は感度出力リクエスト（UTPUT, H3DTOPOL等）と共に用いて、最適化の実行なしにモデルの感度を出力することが可能です。１つの解析ランのみが実行されて、感度計算が完了します。

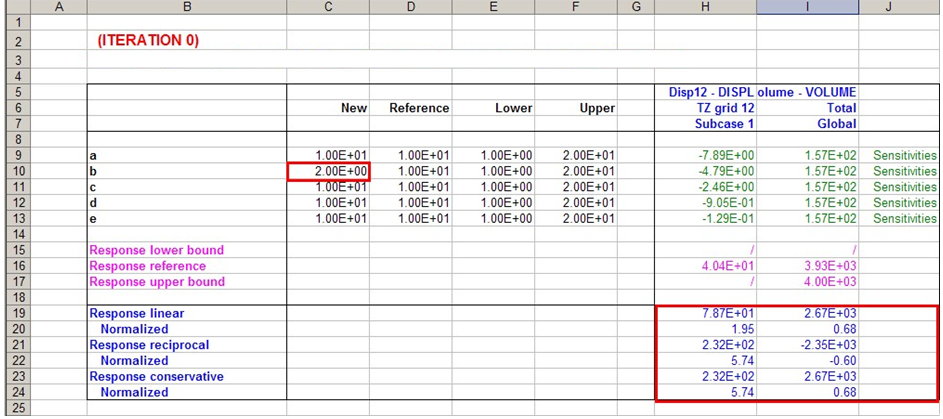
Excelスプレッドシートでは、設計変数を修正し、近似化された応答を計算することが可能です。これは、OptiStructを再度実行することなく設計スタディを作成するために使用することができます。

ムーブリミットの調整

設計変数と中間設計変数（またはそのどちらか）のムーブリミットを使用して、近似の精度を確保します。

近似最適化問題では、設計が最初のポイントから離れるほど、近似値は正確ではなくなります。近似の最適設計は、実際の最適設計からかけ離れたものになるので、これによって全体の収束が遅くなる可能性があります。これは次のようになります。(10)

\underline{X} \leq {\underline{X}}_{m} \leq X \leq {\bar{X}}_{m} \leq \bar{X}

ムーブリミットが小さいほど、スムーズに収束します。繰返し計算ごとに小さな設計変更があるため、多くの繰返し計算が必要となる場合があります。ムーブリミットを大きくすると、重要な制約条件が不正確に計算されるため、実行不可能な設計の間で振動する可能性があります。近似自体が正確な場合には、大きなムーブリミットを使用できます。近似最適化問題における一般的なムーブリミットは、現状の設計変数の値の20％です。高度な近似の概念を使用する場合は、ムーブリミットは最大50％まで可能です。

高度な近似の概念を使用しても、設計変数に関する実際の応答の挙動を十分に近似できない可能性はあります。高精度な近似には大きなムーブリミットを使用し、高精度が要求されない近似には小さなムーブリミットを使用するのが最良の方法です。

すべての応答の近似に対して、設計変数ムーブリミットの同じセットを使用する必要があります。設計を進める応答の近似に注目することが重要です。これらが目的関数であり、最も重要な制約条件です。目的関数が誤った方向に移行する場合や、重要な制約条件に対する違反が増加する場合は、近似が正確ではない兆候です。この場合には、すべての設計変数のムーブリミットを小さくします。ただし、ムーブリミットを小さくしすぎると、最適な設計から程遠い設計変数はゆっくり変化せざるをえないため、収束が遅くなります。したがって、ムーブリミットの中で常に上限または下限に達する設計変数がある場合は、そのムーブリミットを大きくします。ムーブリミットはOptiStructにより自動的に調整されます。

制約条件のスクリーニング

最適化プロセスの各反復計算では、設計問題の目的関数およびすべての制約条件が評価されます。

最適化問題でこれらすべての応答を保持することには、次の２つの潜在的な短所があります。

大量の応答および設計変数を伴う大きな最適化問題となる可能性があります。大半の最適化アルゴリズムは、大量の応答または大量の設計変数を扱うように設計されていますが、その両方を扱うようには設計されていません。
勾配ベースの最適化については、これら応答の設計感度を計算する必要があります。設計感度計算では、大量の応答および大量の設計変数があると、演算処理に大きな負荷がかかります。

制約条件のスクリーニングは、問題の実用的な内容を損なわない範囲で、最適化問題で扱う応答の数を削減するプロセスです。この保持される応答のセットは、最適化問題のサイズを許容しうるレベルに制限する一方で、元の設計問題の本質を捉えています。制約条件のスクリーニングは、同じ指定領域および同じサブケースの範囲内で制約条件のある応答のうち、限界値から遠く離れ、条件を満たす範囲に存在するもの、または同じタイプの多くの応答に比べて重要度の低いもの（上限値に対しては負の小さな値、下限値に対しては正の大きな値）は、最適化問題の方向に影響を与えないという事実を利用しています。スクリーニングにより、これらの応答は現在の設計の反復の問題から除外されます。

100,000個の要素からなる有限要素モデルを扱う最適化問題について考えます。この問題の目的は、モデルの要素にかかる応力を材料の降伏応力以下に維持できる範囲で、モデルの質量を最小化することです。この問題では、サブケースごとに100,000の制約条件（各要素にかかる応力は使用材料の降伏応力より小さいこと）があります。各設計変数について、すべての反復計算で、サブケースごとに100,000回の感度計算を行う必要があります。設計変数の変化はムーブリミットの調整で制限されているため、ある反復計算から次の反復計算の間で、応力が急激に変化することはありません。したがって、使用材料の降伏応力よりはるかに小さい応力だけがかかる要素の感度を計算するのは無駄です。また、最適化の方向は、最も高い要素応力でほとんど決まります。したがって、必要な計算の数は、最大の応力がかかる要素を適切な数だけ考慮することにより、大幅に削減できます。

当然のことながら、制約条件のスクリーニングを使用することには代償があります。一部の制約条件の応答を考慮しないことにより、収束解に到達するには、より多くの反復計算が必要になる場合があります。スクリーニングされる制約条件の応答が多すぎる場合、収束解を得るまでに長時間を要することがあります。スクリーニング後の応答の数が、最適化問題でアクティブな制約条件の数より小さいと、最悪の場合、解が収束しないこともあります。

大規模なテストにより、大多数の問題では、制約条件をスクリーニングすることにより、多くの時間と計算の手間を省略できることが判明しています。そのため、OptiStructでは、制約条件のスクリーニングがデフォルトでアクティブとなっています。デフォルトの設定では、サブケースごと、領域ごと、応答タイプごとに、境界値の範囲内で条件を満足する側の50％に入る、最も重要な（上限に対してはほとんどが正の値であり、下限に対してはほとんどが負の値をとる）20の制約条件のみを考慮します。

DSCREENバルクデータエントリで、スクリーニングのしきい値と保持される制約条件の数の両方が制御されます。DRESP1バルクデータエントリによりサポートされているすべての応答タイプで、異なるDSCREEN設定が可能です。DRESP2バルクデータエントリで定義される応答は、RTYPE=EQUAが指定されている単一のDSCREENエントリで制御されます。同様に、DRESP3バルクデータエントリで定義される応答は、RTYPE=EXTERNALが指定されている単一のDSCREENエントリで制御されます。同じ領域識別子を使用するDRESP2およびDRESP3定義で、同様の数式が使用されるようにすることが重要です（制約条件のスクリーニングが効果的に機能するためには、同じ領域内の応答が同じ程度の大きさをもち、同じ程度の感度を示している必要があり、それを確実にするための最も簡単な方法は、同様の変数の組み合わせを使用することです）。

安定した収束を得るのに必要な最小応答数を保持する目的で、スクリーニングの条件を自動的かつ適切に調整することが可能です。DSCREENバルクデータエントリの代替フォーマット上で２番目のフィールドをAUTOとすることで、この機能が有効となります。領域の定義もこの設定で自動化されます。この設定は、初心者のユーザーに有用で、局所的な制約条件が数多く存在する場合に特に役立ちます。ただし、設定には次のような幾つかの制限事項があります；　上級のユーザーは、スクリーニングの条件を手動で定義することで、より良いパフォーマンスが得られるかもしれません。AUTOで実行するには、より多くのメモリが必要となる場合があります。手動により制約条件を低く抑えると、メモリが少なく済むため、非常に大きい問題には（収束の安定性と最適性について妥協しても）望ましいかもしれません。LEVELフィールドを介して5つのレベルの自動スクリーニング（AUTO）が可能です。自動スクリーニングを完全にOFFにするには、LEVELフィールドをOFFにセットします。

最適化に座屈固有値が含まれている場合、自動スクリーニング機能（AUTO）は以下の設定を自動的に調整します。

DOPTPRM,GBUCK,1は、ユーザーによりオンと設定されていない場合はオンに切り替えられ、最も低い15の座屈モードが最適化で考慮されます。これは、収束の安定化を向上させる一助となります。最も低い、もしくは少数の座屈固有値のみを制約すると、収束は不安定となります。これは、反復計算が進むのに連れて座屈モードが変化し得るためで、保持された座屈モードもまた変化し得ることを意味します。より良い定式化は、最も低い10～15モード（どれだけのモードが境界に近づくかにより、それ以上もあり得る）を制約することです。
EIGRLカードの上限は、座屈固有値のみを計算するために調整され、これは最適化で保持される可能性があります。パフォーマンスを向上させるために、OptiStructは、境界からかけ離れた（すなわち安全ゾーンにある）座屈固有値を計算することを回避します。

自動スクリーニング（上記の座屈調整を含む）は、DCREEN,AUTO,OFFをセットすることにより完全に無効にできます。しかしながら、座屈の自動スクリーニングのみを無効とする（応力などの局所応答について自動スクリーニングを保持したい際に必要となる場合がある）際は、DSCREENエントリのBUCK（4番目の）フィールドでNOBUCKオプションを指定することが可能です。

領域とその目的

OptiStructにおいて、領域とは同じタイプの応答のグループです。

領域は、応答の定義に使用するDRESP1バルクデータエントリ、DRESP2バルクデータエントリ、およびDRESP3バルクデータエントリの領域識別子フィールドで定義されます。領域識別子フィールドが空白のままの場合、応答に関連する各特性が、それ自身の領域を形成します。異なるタイプの応答に、同じ領域識別子を使用することもできますが、それらの応答はタイプが異なるので、同じ領域を形成することはできません。

例1

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
DRESP1	1	label	STRESS	PSHELL		SMP1		1
	2	3

ID 1のDRESP1は、PID 1、2または3のPSHELL定義を参照するすべての要素の応力応答を定義します。領域識別子は定義されていないため、各PSHELLの応力応答は、独自の領域を形成します。よって、PID1のPSHELLを参照する要素のすべての応力応答は、PID2のPSHELLを参照する要素のすべての応力応答と異なる領域にあります。また、PID2のPSHELLを参照する要素のすべての応力応答は、PID3のPSHELLを参照する要素のすべての応力応答と異なる領域にあります。この応答の定義が最適化問題で制約されていて、デフォルトの制約条件スクリーニングが実行されるとすると、3つのPSHELL定義のそれぞれに対して20の要素応力が考慮されます。すなわち、保持される応答は、それぞれの領域について20で、全部で60となります。

例 2

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
DRESP1	2	label	STRESS	PSHELL	1	SMP1		1
	2

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
DRESP1	3	label	STRESS	PSHELL	1	SMP1		3

上記のDRESP1エントリで定義されるすべての応力応答は、単一の領域を形成します。フィールド6のエントリが空白でないことにご注目ください。ここで、同じタイプ（STRESS）で、フィールド6に空白でない同じエントリを持つこれらの応答定義が、最適化問題で制約され、デフォルトの制約条件スクリーニングが実行されるとすると、すべて単一の領域を形成しているため、３つのPSHELL定義に対して全部で20の要素応力が考慮されます。

離散設計変数

ある一定の範囲で薄板の厚みが指定されている場合のように、離散値には連続的な傾向があります。

OptiStructでは、寸法および形状の最適化の場合、勾配ベースの最適化アプローチを使用します。複合材の積み重ねシーケンスを最適化する場合の設計変数のように、離散値をとる設計変数では、この方法は良好に機能しません。この方法は、離散値の間隔が小さい場合に、最もよく機能します。すなわち、設計問題の挙動が連続的であるほど、離散的な解の信頼性は高くなります。たとえば、厚みの変数に0とTの２つの離散値が与えられている場合、満足できるパフォーマンスは期待できません。

分岐や境界など、厳密さが要求される方法は、演算時間が非常に長くなることが知られています。そこで、比較的大きなサイズの問題を効果的に解くことに的を絞った、半直感的な方法が開発されました。ベースラインの連続解を比較対象として、離散設計のベンチマーク評価を行うことをお奨めします。これにより、離散変数によるトレードオフを定量化でき、離散的な解が妥当かどうかを把握できます。非凸最適化問題では、局所的な最適条件の存在は必ず障害になりますが、離散変数によって、この問題はさらに深刻なものになりがちです。特に解の最適性に疑義がある場合は、１つの設計問題を、いくつかの異なる出発点から開始してみると有効な場合があります。

最適化問題で、これらの離散変数を連続変数と組み合わせて使用することも可能です。

離散設計変数は、DESVARカードのDDVALエントリを参照することによりアクティブになります。

DOPTPRMカードのDDVOPTパラメータでは、完全な離散最適化、または、まず連続最適化が実行され、次に連続最適設計から離散最適化が開始される２段階アプローチのいずれかを選ぶことができます。

MFD、SQP、DUAL、BIGOPT 、DUAL2を含むすべての最適化アルゴリズムは、離散設計変数を伴う最適化問題をサポートしています。MFDは、散設計変数を伴うモデルでデフォルトのアプローチとなっています。