OS-V：0830 Chaboche複合硬化材料を使用した非線形静解析

ラチェッティングの予測では、材料硬化パラメータの正確な指定が不可欠です。Chaboche硬化パラメータを使用して、OptiStructによってラチェッティングの数値シミュレーションが実行されました。その後で、数値結果が、応力制御の繰り返し荷重テストで得られた実験データと比較されました。

ベンチマークモデル

大きさが0.02mmのX方向の強制変位は、図1（右）に示すように、節点ID（2、3、6、および7）でX方向と垂直に与えられます。

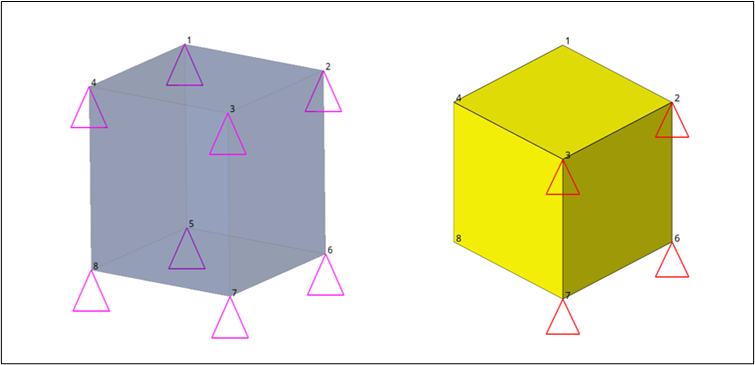
図 1. 境界条件が設定されたモデル. 左：拘束、右：強制変位

繰り返し塑性は、閉じられた繰り返し荷重経路での材料の弾塑性応力ひずみ応答に関します。繰り返し塑性現象の中で、ラチェッティングは、材料にさらに損傷を与え、その疲労寿命を短くする可能性があります。ラチェッティングは、平均応力がゼロ以外の応力制御繰り返し荷重の下で材料内に次第に蓄積されるひずみとして定義されます。試験体は左端で縦方向に拘束され、強制変位が右端に適用されます。時間依存の強制変位が使用されます（図2）。

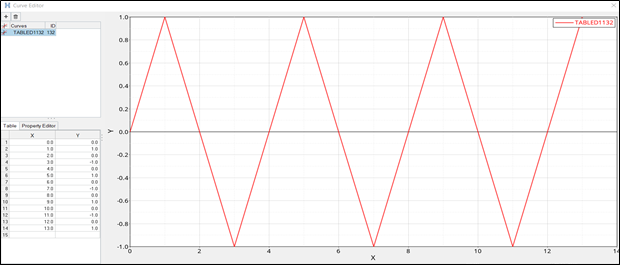
図 2. 時間依存の強制変位

材料

PA6アルミニウムと複合硬化材料の特性：

Chabocheモデルでは、3つの非線形項とVoce等方性を使用して、PA6アルミニウムのラチェッティングがシミュレートされます。Chabocheモデルの硬化パラメータは、ひずみ制御の繰り返し引張 / 圧縮テストで得られた実験応力ひずみ曲線に基づいて決定されます。

MAT1

ヤング率（E）

71000 MPa

ポアソン比（u）

0.33

MATS1

MAT1エントリの特定（MID）

21

硬化則（HR）

6

移動硬化特性

NLKIN

移動硬化に関するデータ入力。

移動硬化の背応力の数（NKIN）

3

初期降伏応力（SIGY0）

410.0 MPa

Ci

MPA内のNLKINの背応力成分のパラメータCi（PARAM）。

C1

4735.0

C2

1511.0

C3

1554.0

Gi

NLKINの背応力成分のパラメータGi（PARAM）。

G1

299.0

G2

291.0

G3

22.0

等方硬化

NLISO

等方性硬化に関するデータ入力。

初期降伏応力（SIGY0）

410.0

NLISOのパラメータQ（Q）

150.0 MPa

NLISOのパラメータB（B）

11

結果

結果では、実験による応力ひずみ曲線と、最小二乗法による最適化後のChabocheモデルの数値的な応力ひずみ曲線が比較されます。

図 3. 参照結果

OptiStructの結果の要素の応力ひずみグラフ（左）とPA6アルミニウムの実験の応力ひずみ曲線（右）を図4に示します。

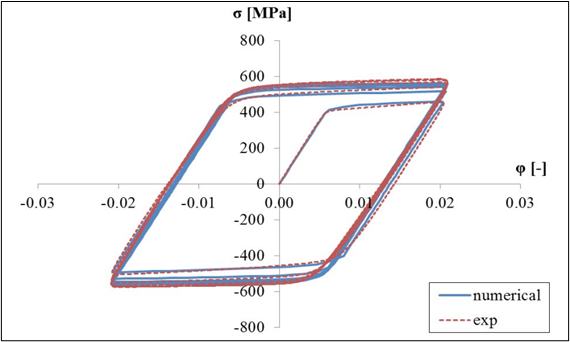
図 4. OptiStructの結果

複合硬化材料モデルを使用してOptiStructから得られた結果は、実験結果に似ています。

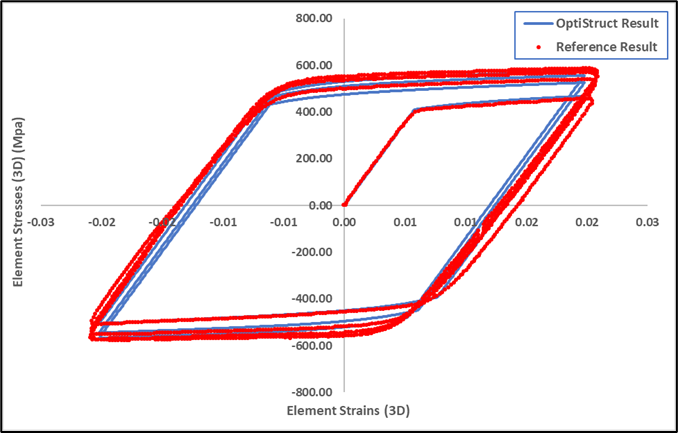
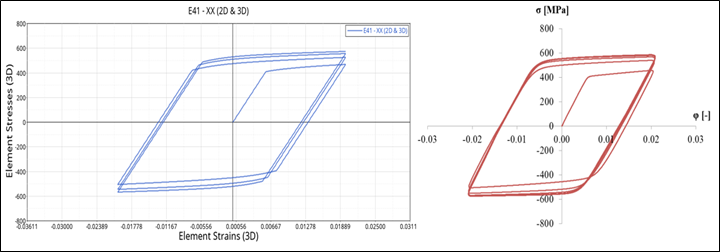
図 5. 重ね合わせた参照結果とOptiStructの結果

図5は、OptiStructの結果と参照結果の一致を示しています。OptiStructの結果の曲線は、参照結果の曲線と完全に重なっています。

モデルファイル

必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。