OS-V:0820 粘弾性を備えたMarlow超弾性材料モデル
超弾性材料モデルと粘弾性の組み合わせによって、ひずみ速度に依存した大ひずみ応答をモデル化できます。
Marlowモデルは、少数のモデルパラメータを使用せずに1つのスカラー関数を使用して機械的特性を設定するという点で、ほとんどの超弾性モデルと異なります。パラメータの調整を使用せずに応力-伸長(伸長=工学ひずみ+1)曲線を指定することで、Marlowモデルを容易に定義できます。Marlowモデルと粘弾性の組み合わせは、高精度で使いやすいひずみ速度依存型超弾性モデルを作成する手法です。この組み合わせの場合、Marlowモデルでは、瞬時材料応答または長期的材料応答を得るために応力-伸長曲線が必要になりますが、実験で得られるデータは有限なひずみ速度での値に限られます。
ベンチマークモデル
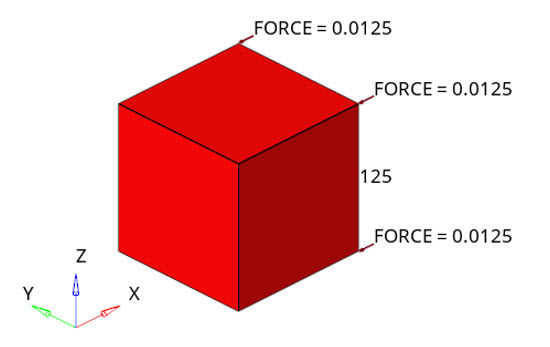
図 1. 荷重を伴うベンチマークFEMモデル
この単一のCHEXA8要素モデルはエッジの長さが1.0mmです。このMarlowモデルは、データの単一なセットを使用するだけで実験データから得られます。単軸引張試験、単軸圧縮試験、等二軸試験、または平面試験の形式による試験データを使用します。偏差挙動は、1回目の伸長不変量のみに依存し、2回目の不変量には依存しません。
材料
- 特性材料
- 値
- 密度
- 1 x 10-9トン/mm3
- ポアソン比
- 0.499
モデルファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
- MATHE-Marlow_tension.fem
- MATHE-Marlow_compression.fem
- MATTHE-Marlow.fem
- MATHE-VE-Marlow.fem
- MATTHE-VE-Marlow.fem
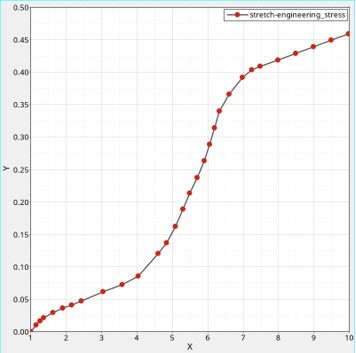
MATHE引張
超弾性材料モデルでは、ひずみエネルギー密度を変形状態の関数として定式化することで、非線形弾性挙動を表現します。この弾性ポテンシャルは、ひずみ不変量(, , )または主伸長(, , )の関数として表現します。一般に超弾性モデルは、材料定数または実験データを使用して指定できます。
引張入力データで対応できる工学応力は最大で0.46MPaまでです。設計荷重は公称応力0.5MPaに相当しているので、NLSTAT LGDISP荷重ステップの最後では外挿を使用します。

図 4. ポアソン比、材料密度、表の参照
結果
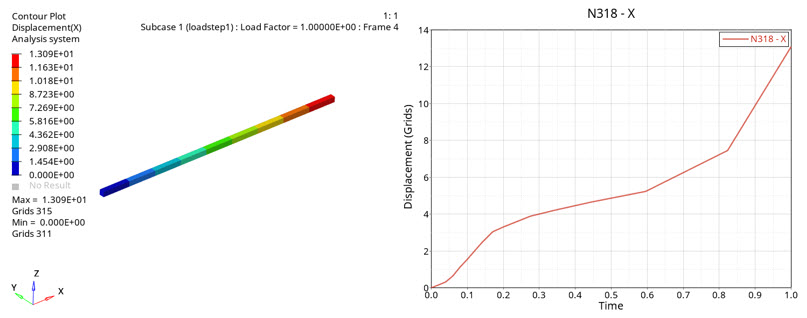
図 5. 引張力に起因するCHEXA要素の変形
MATHE圧縮
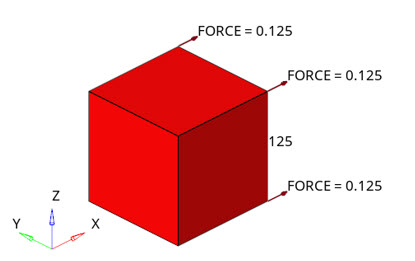
図 6. 圧縮力を適用したCHEXA要素モデル
力によって公称圧縮応力0.05MPaを適用します。このモデルは単純に支持されています。
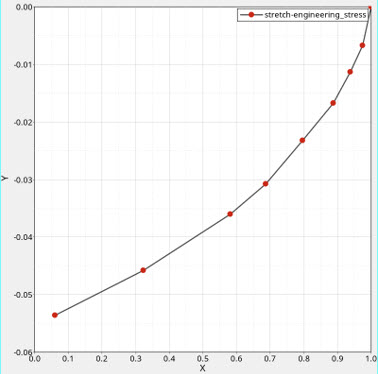
図 7. 実験に基づく圧縮応力-伸長曲線
圧縮時には、伸長量はの範囲で設定でき、モデルの変形は指定の範囲に収まります。
結果
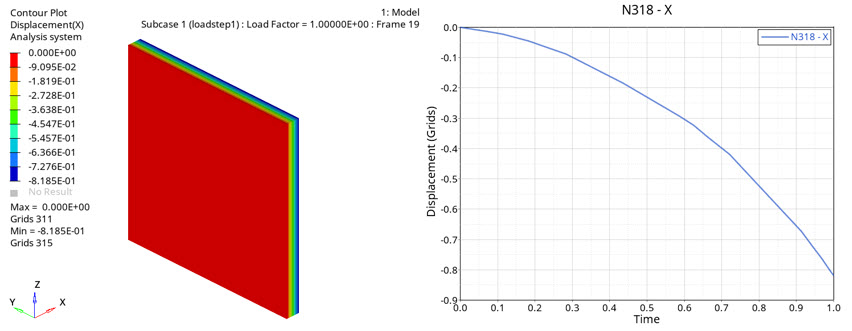
図 8. 圧縮力に起因するCHEXA要素の変形
MATTHE
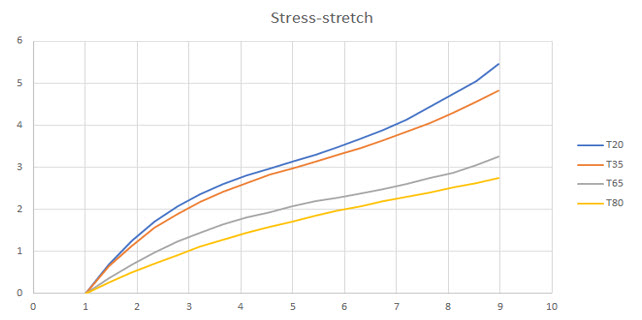
図 9. 各温度における実験に基づく応力-伸長データ

図 10. MATTHE Marlow材料モデルの指定
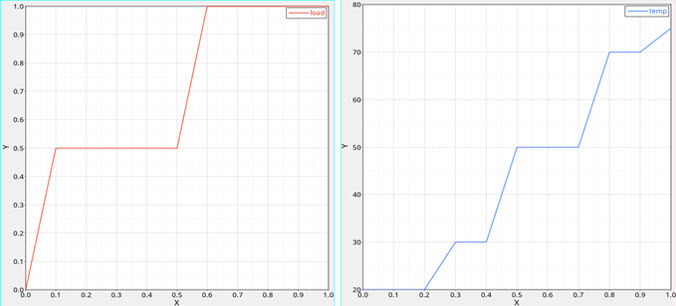
図 11. CHEXA要素に適用した機械荷重(左)と熱荷重(右)
このサンプルモデルには、さまざまなフェーズで進展する機械荷重プロファイルと熱荷重プロファイルを定義した2つのTLOAD1が設定されていて、DLOADと組み合わされます。
結果
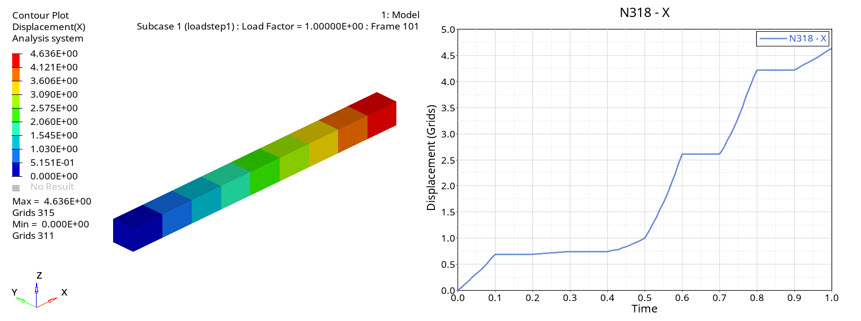
図 12. CHEXA要素の変形. 荷重方向への変位
MATHE+VE
超弾性Marlowモデルと粘弾性の組み合わせによって、Marlow手法の利点を維持しながら、ひずみ速度に依存する材料挙動を表現できます。ここでいうMarlow手法の利点とは、試験データを直接使用した簡便な設定と、試験データの正確なモデリングです。粘弾性モデルを使用すると、緩和およびひずみ速度依存の弾性特性を表現できます。
- せん断応力
- せん断ひずみ
- 緩和関数
| (s) | (s) | (s) | (s) | (s) | GPaのK | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.3539 | 0.08124 | 0.07458 | 1.692 | 0.05052 | 35.23 | 0.04117 | 733.5 | 0.04575 | 15275 | 2.5 |
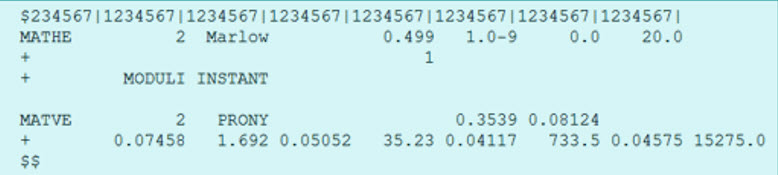
図 13. 粘性超弾性モデルを対象にした同じIDのMATHE + MATVEカード指定
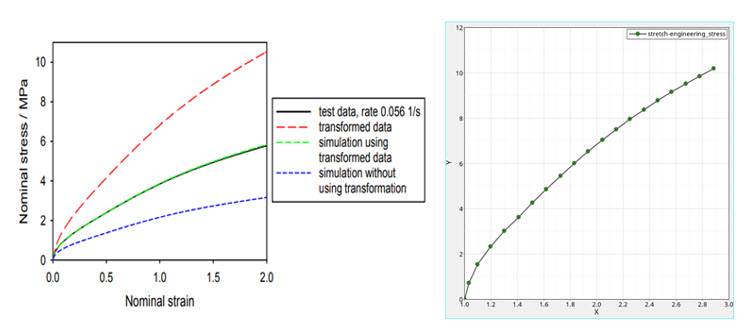
図 14. 瞬時応力-ひずみ曲線(左)と、それに対応するMATHEカードの応力-伸長曲線(右)
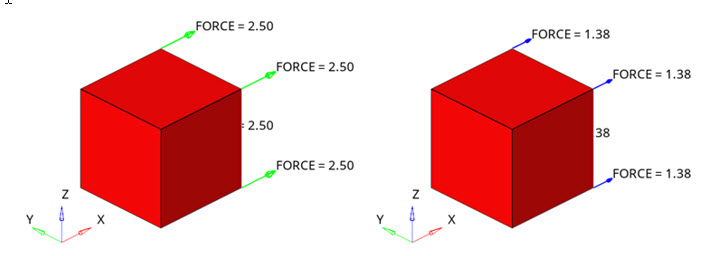
図 15. 荷重と荷重速度が異なる2つの荷重ステップ
単一要素モデルには、ゼロから公称応力までの単軸荷重を適用します。公称応力が10.0MPaである1番目の荷重ステップでは0.02秒間で応力が増大し(左)、公称応力が5.5MPaである2番目の荷重ステップでは200秒間で応力が増大しています(右)。
結果
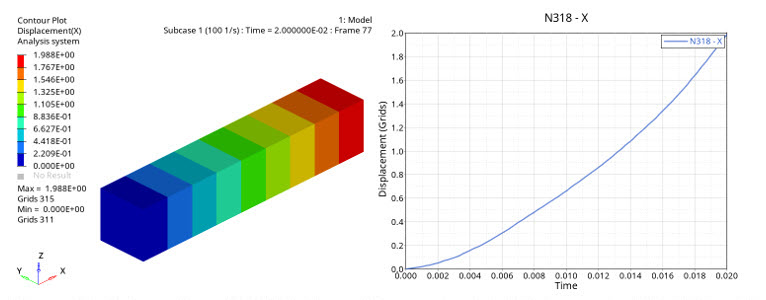
図 16. 0.02秒以内に無荷重状態から公称応力の10.0MPaに達するCHEXA要素の変形
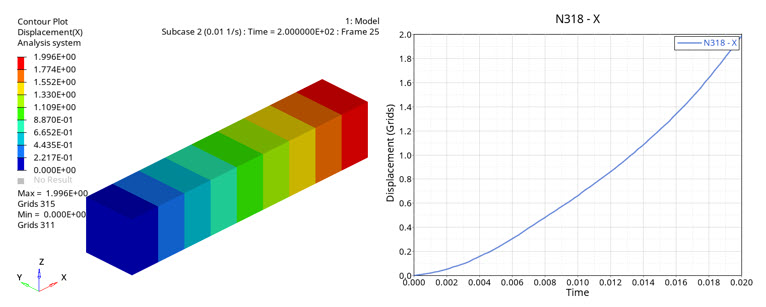
図 17. 200秒以内に無荷重状態から公称応力の5.5MPaに達するCHEXA要素の変形
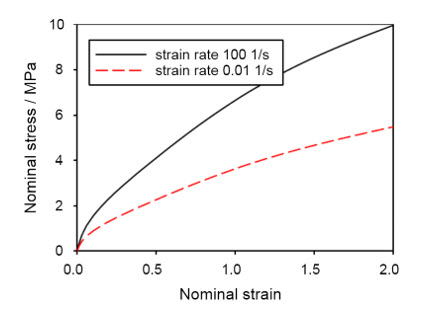
図 18. 基準結果
MATTHE+VE
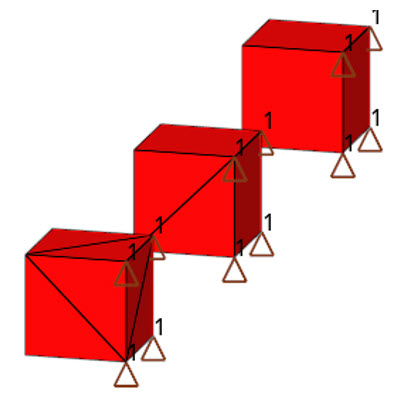
図 19. モデル要素CTETRA、CPENTA、CHEXA
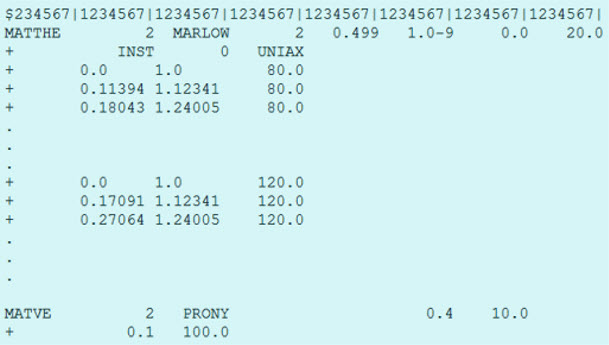
図 20. 温度依存のMATTHE Marlowモデル
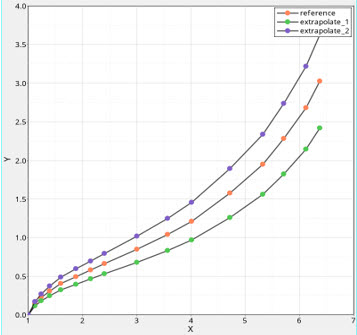
図 21. 材料の応力-伸長データ
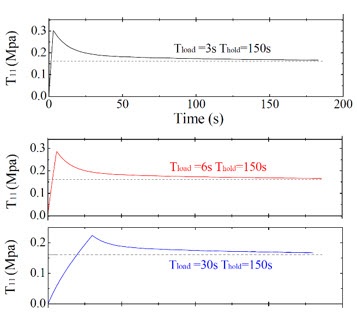
図 22. 3秒、6秒、30秒のTloadを適用した基準結果
2種類の外挿環境における単軸引張データを入力データとして使用します。
結果
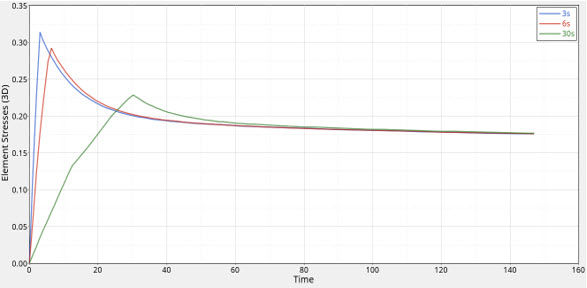
図 23. 3秒、6秒、30秒のTloadを適用した要素応力