OS-V: 0530 Composite Shell Bending
This problem discusses about the composite shells two- or three-layer plate subjected to a sinusoidal distributed load, as described by Pagano (1969).
The resulting transverse shear and axial stresses through the thickness of the plate are compared to analytical solutions using classical laminated plate theory (CPT) and linear elasticity theory.
Benchmark Model
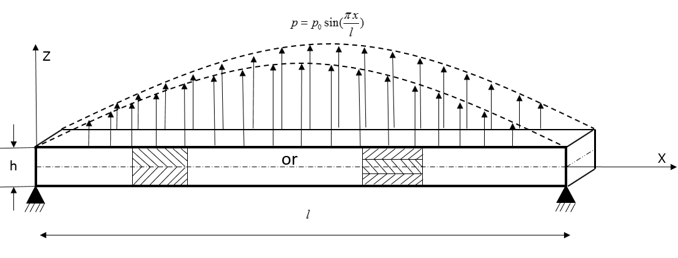
図 1. Composite Shell Subjected to Uniformly Varying Sine Load
- For the two-layer model, top layer is in 90° and bottom layer is in 0°.
- For the three-layer model, the top and bottom layer are in 0° orientation and the middle ply is in 90° orientation.
- Property
- Value
- EL
- 25*106 lb/in2 (172.4 GPa)
- ET
- 1.0*106 lb/in2 (6.90 GPa)
- GLT
- 0.5*106 lb/in2 (3.45 GPa)
- GTT
- 0.2*106 lb/in2 (0.2 GPa)
- VLT = VTT
- 0.25
- L
- Signifies the direction parallel to the fibers
- T
- Signifies the transverse direction
| Stress Value | Xt | Xc | Yt | Yc | S |
|---|---|---|---|---|---|
| GPa | 2.07*10-4 | -8.28*10-5 | 3.45*10-6 | -1.03*10-5 | 6.89*10-6 |
| lb/in2 | 30.0 | -12.0 | 0.5 | -1.5 | 1.0 |
Results
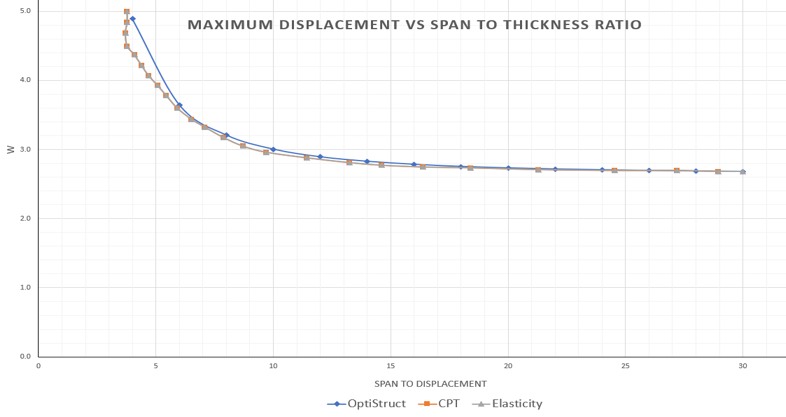
図 2. Maximum Displacement versus Span to Thickness Ratio of Two-layer 2nd Order Plate
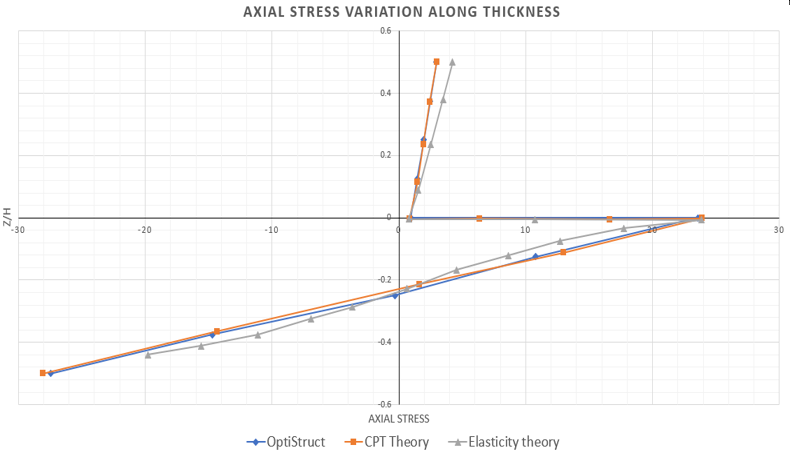
図 3. Axial Stress Distribution through the Thickness of Two-layer 2nd Order Plate
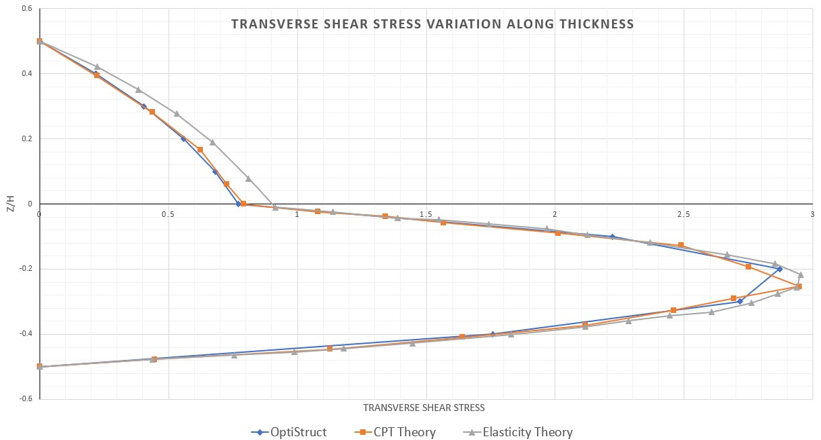
図 4. Transverse Shear Stress Distribution through the Thickness of Two-layer 2nd Order Plate
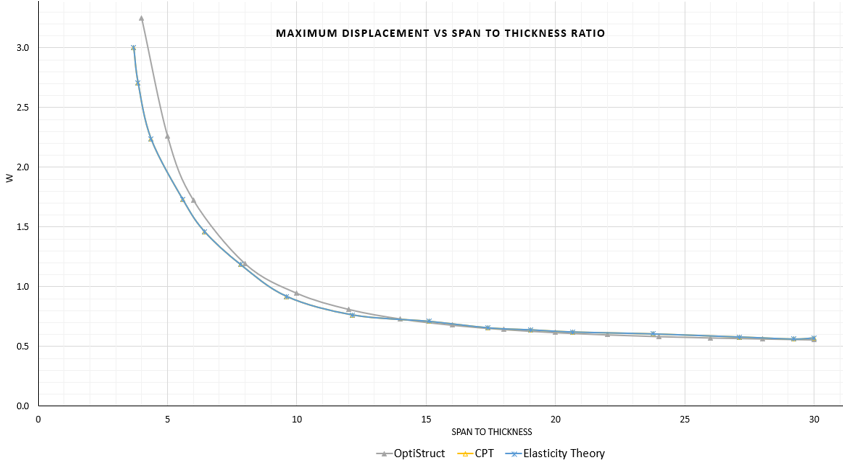
図 5. Maximum Displacement versus Span to Thickness Ratio of Three-layer 1st Order Plate
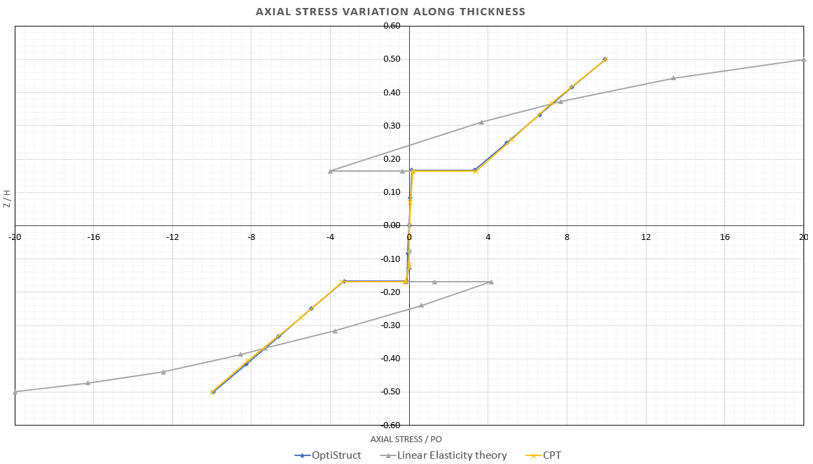
図 6. Axial Stress Distribution through the Thickness of Three-layer 1st Order Plate
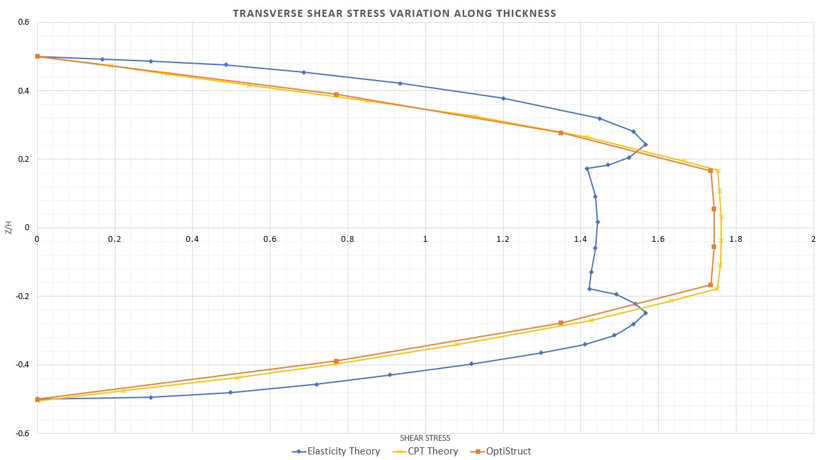
図 7. Transverse Shear Stress Distribution through the Thickness of Three-layer 1st Order Plate
Model Files
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
- composite-shells-2-plys-2nd-order-span-4.fem
- composite-shell-1st-order_span-4.fem
Reference
Exact Solutions for Composite Laminates in Cylindrical Bending by N.J. Pagano, Washington University, St. Louis, MO (May 7, 1969)
Nonlinear finite element shell formulation accounting for large membrane strains by Thomas J.R. Hughes and Eric Carnoy, Stanford University (1982)