Parametric Model Class
Contains the model design parameter values and the methods for generating a model, adding responses, performing the optimization, and printing results.

| init | Creates an instance of the parametric class. |
| createModel | Creates a designable model that can be provided to the optimizer. |
| addResponses | Adds responses to the designable model. These are used for cost and constraint definition. |
| simulate | For debug purposes only. This method will perform a simulation and make sure the designable model runs without any issues. |
| optimize | Performs an optimization. |
| printResults | Prints the results you want to see to the screen and to the log file. |
| main | Invokes the various methods to perform a simulation. |
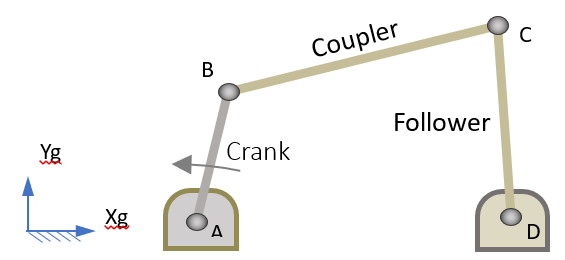
Figure 1.
- R is at Point A
- S is at Point B
- U is at Point C
- R is at point D
The two revolute joints at A and D are defined with their Z-axes along the global Z.
The spherical joint at B does not care about orientations.
- 1st z-axis, zi, along global Z
- 2nd z-axis, zj, perpendicular to zi and the line from B to C
The entire model is parameterized in terms of these four design points: A, B, C and D.
Operating in 2D space, this leads to eight design variables: ax, ay, bx, by, cx, cy, dx and dy.
| DV | Value | (bi, bu) |
|---|---|---|
| ax | -45 | (-50 ,50 ) |
| ay | +45 | (-50 ,50 ) |
| bx | +65 | (+20 ,80 ) |
| by | +260 | (+180,280) |
| cx | +300 | (+240,380) |
| cy | +500 | (+400,620) |
| dx | +515 | (+180,520) |
| dy | -85 | (-100,20 ) |
class Fourbar (object):
def __init__ (self, ...)
...
def createModel (self):
...
def addResponses (self):
...
def simulate (self):
...
def optimize (self):
...
def printResults (self):
...