OS-T: 1370 Complex Eigenvalue Analysis of a Reduced Brake System
In this tutorial, a modal complex eigenvalue analysis is performed on a simplified brake system to determine whether the friction effects can cause any squeal noise (unstable modes).
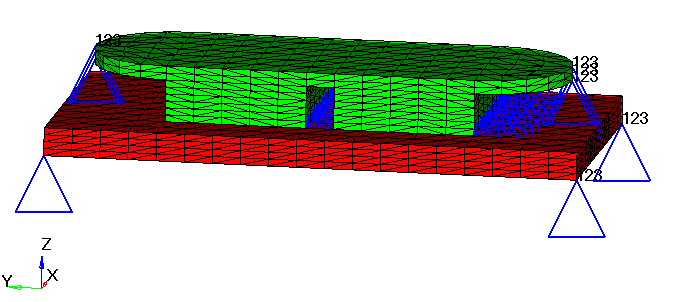
Figure 1. Model Review
Launch HyperMesh and Set the OptiStruct User Profile
Import the Model
Set Up the Model
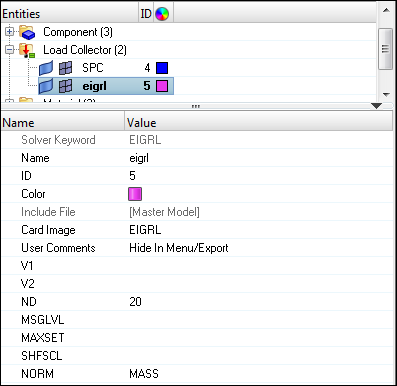
Create EIGRL and EIGC Cards
Retrieve Friction Data and Define Analysis Parameters
Retrieve the friction coefficients from the DMIG.pch file.
Define a Load Step for Modal Complex Eigenvalue Analysis
- In the Model Browser, right-click and select .
- For Name, enter complex_eigen.
- Click Analysis type and select Complex eigen (modal) from the drop-down menu.
- For SPC, click .
- In the Select Loadcol dialog, select SPC from the list of load collectors and click OK.
- For CMETHOD, click .
- In the Select Loadcol dialog, select eigc from the list of load collectors and click OK.
- For METHOD(STRUCT), click .
- In the Select Loadcol dialog, select eigrl from the list of load collectors and click OK.
 .
.