OS-V: 0820 Marlow Hyperelastic with Viscoelasticity Material Model
The combination of hyperelastic material models with viscoelasticity allows to model the strain rate dependent large strain response.
The Marlow model differs from most hyperelastic models by the concept not to use a small number of model parameters, but a scalar function to define the mechanical properties. It can be defined conveniently by providing the stress–stretch (stretch = engineering strain+1) curve without needs for parameter calibration. The coupling of the Marlow model and viscoelasticity is an approach to create a strain rate-dependent hyperelastic model which has good accuracy and is convenient to use. In this combination, the Marlow model requires to specify the stress–stretch curve for the instantaneous or long-term material response, while experimental data can be obtained only at finite strain rates.
Benchmark Model
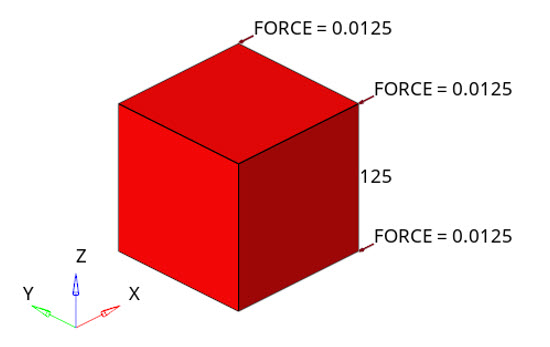
Figure 1. Benchmark FEM model with loads
The single CHEXA8 element model has an edge length of 1.0 mm. The Marlow model is derived from experimental data only using a single set of data. The test data in the form of uniaxial tension, uniaxial compression, equi-biaxial, or planar test is used. Deviatoric behavior depends on the 1st stretch invariant only and it is independent of the 2nd invariant.
Materials
- Property Material
- Values
- Density
- 1 x 10-9 tonnes/mm3
- Poisson's ratio
- 0.499
Model Files
Refer to Access the Model Files to download the required model file(s).
- MATHE-Marlow_tension.fem
- MATHE-Marlow_compression.fem
- MATTHE-Marlow.fem
- MATHE-VE-Marlow.fem
- MATTHE-VE-Marlow.fem
MATHE Tension
Hyperelastic material models describe the nonlinear elastic behavior by formulating the strain energy density as a function of the deformation state. This elastic potential is expressed as a function of either the strain invariants (, , ) or the principal stretches (, , ). Generally, hyperelastic model can be specified either with material constant or experimental data.
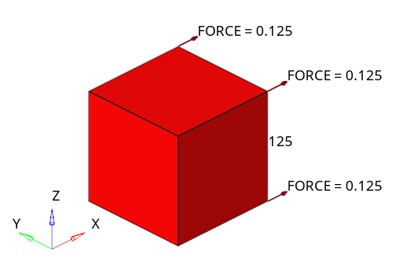
Figure 2. CHEXA element model with applied tensile forces
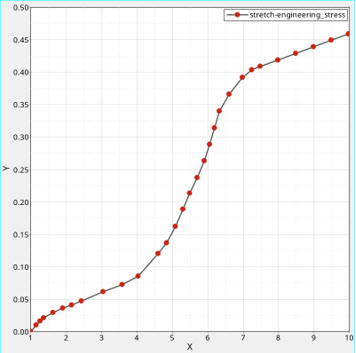
Figure 3. Experimental uniaxial tensile stress-stretch curve
Tensile input data covers engineering stress up to 0.46 MPa and since the design load corresponds to nominal stress of 0.5 MPa, extrapolation is used at the end of the NLSTAT LGDISP load step.

Figure 4. Poisson’s ratio, and density of material and reference to the table
Results
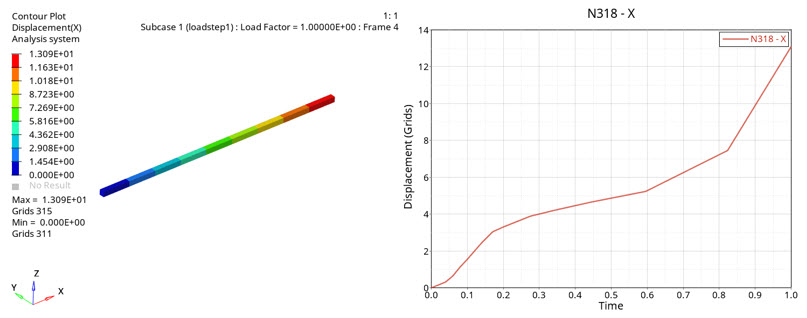
Figure 5. Deformation of CHEXA element due to tensile forces
MATHE Compression

Figure 6. CHEXA element model with compressive forces
The nominal compressive stress of 0.05 MPa is applied with forces. The model is simply supported.
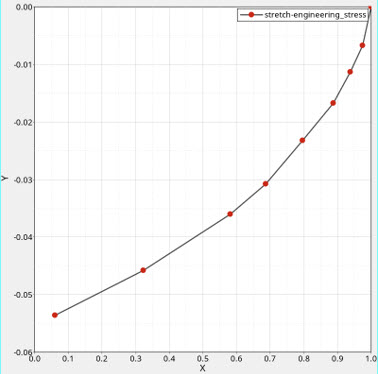
Figure 7. Experimental compressive stress-stretch curve
In compression, stretch can be defined as and the deformation of the model stays in the specified range.
Results
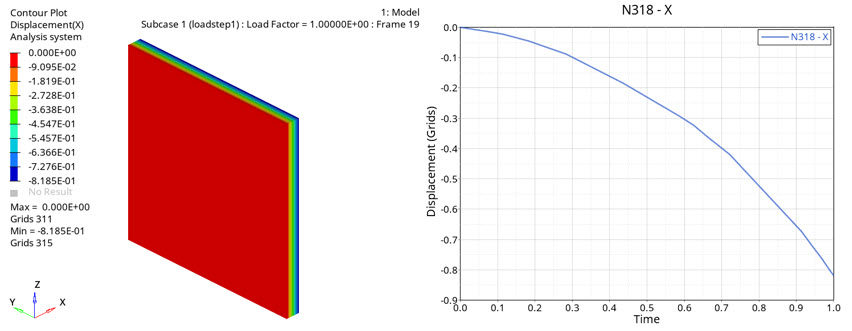
Figure 8. Deformation of CHEXA element due to compression forces
MATTHE
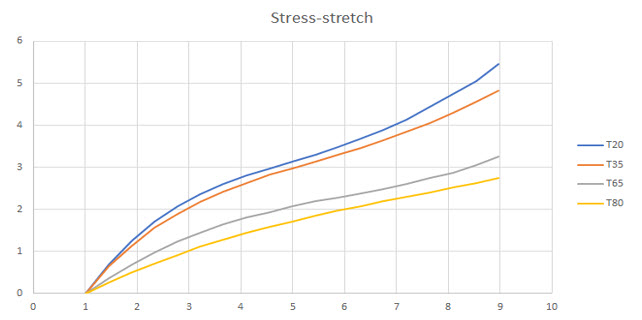
Figure 9. Experimental stress-stretch curve at each temperature

Figure 10. Specify the MATTHE Marlow material model
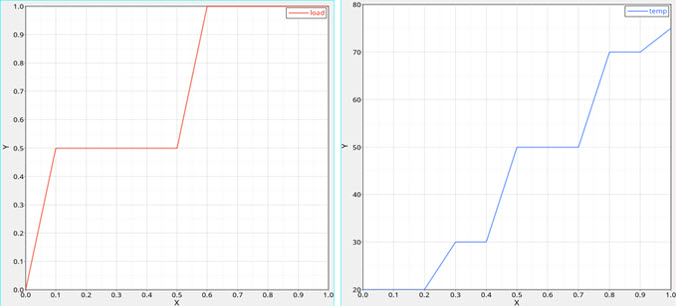
Figure 11. Mechanical load (left) and Thermal load (right) applied on CHEXA element
The example model contains two TLOAD1s that define mechanical and thermal load profiles that evolve in different phases and those are combined with DLOAD.
Results
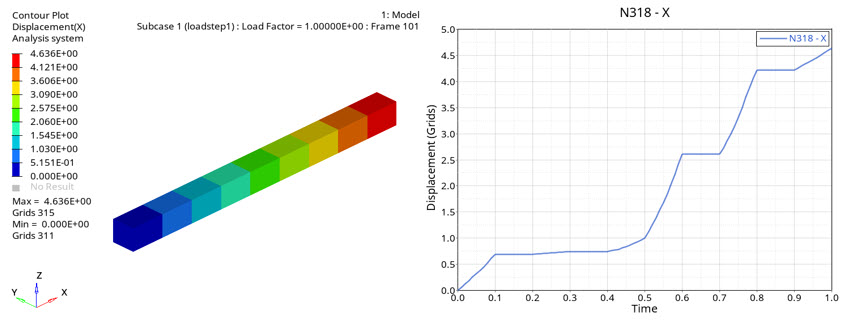
Figure 12. Deformation of CHEXA element. displacement in loading direction
MATHE+VE
A combination of the hyperelastic Marlow model with viscoelasticity provides the capability to describe the strain-rate-dependent material behavior while preserving the advantages of Marlow’s approach, the convenient definition using test data directly and the exact modeling of the test data. Viscoelastic models allow to describe relaxation and strain-rate-dependent elastic properties.
- Shear stress
- Shear strain
- Relaxation function
| in s | in s | in s | in s | in s | K of GPa | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.3539 | 0.08124 | 0.07458 | 1.692 | 0.05052 | 35.23 | 0.04117 | 733.5 | 0.04575 | 15275 | 2.5 |
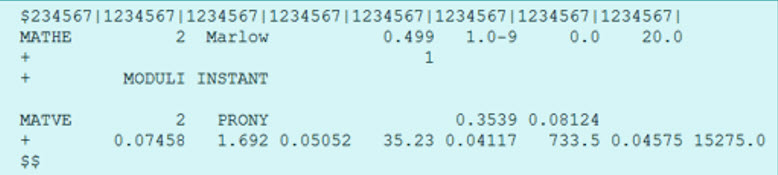
Figure 13. MATHE + MATVE card specification with same ID for visco-hyperelastic model
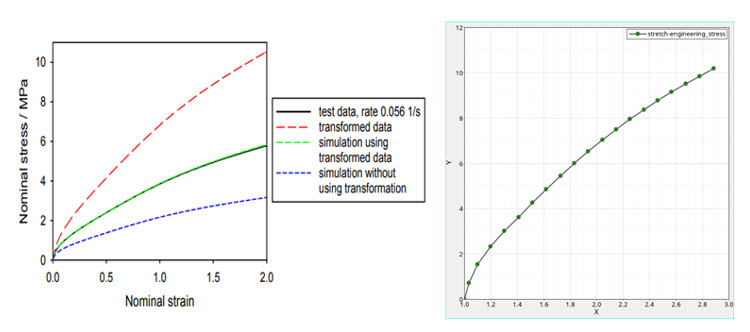
Figure 14. Instantaneous stress-strain curve (left) and the corresponding stress-stretch curve for the MATHE card (right)
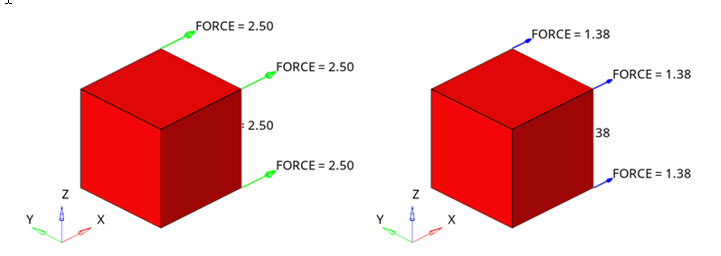
Figure 15. Two loadsteps with different loads and loading rates
Single element model is uniaxially loaded from zero to nominal stress. First loadstep having 10.0 MPa of nominal stress ramped within 0.02s (left) and second loadstep with 5.5 MPa of nominal stress ramped within 200s (right).
Results
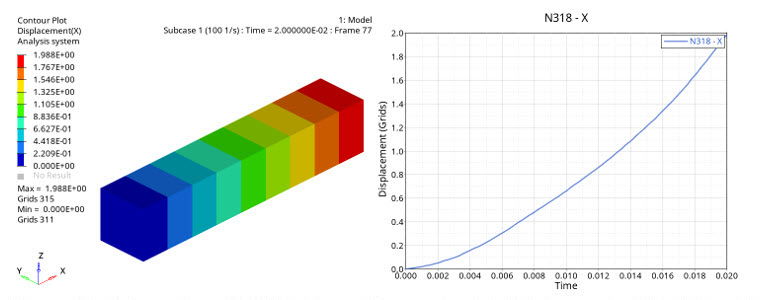
Figure 16. Deformation of CHEXA element from unloaded state to nominal 10.0 MPa within 0.02s
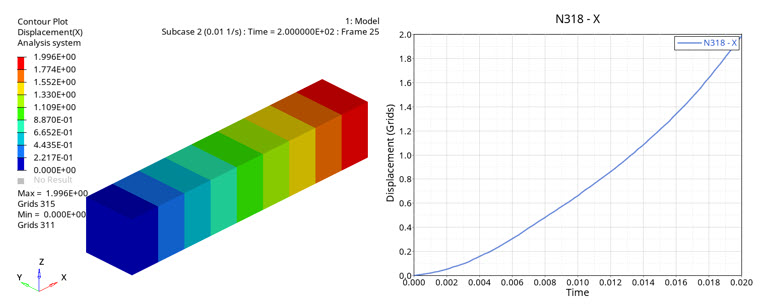
Figure 17. Deformation of CHEXA element from unloaded state to nominal 5.5 MPa within 200s
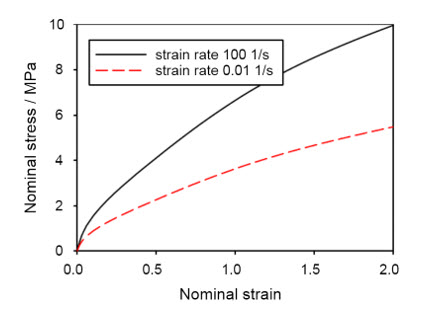
Figure 18. Reference results
MATTHE+VE
Figure 19. CTETRA, CPENTA and CHEXA model elements
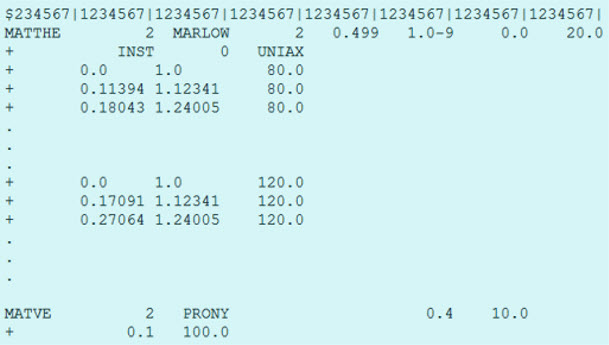
Figure 20. Temperature dependent MATTHE Marlow model
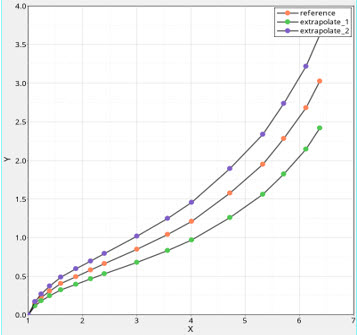
Figure 21. Stress-stretch data of the material
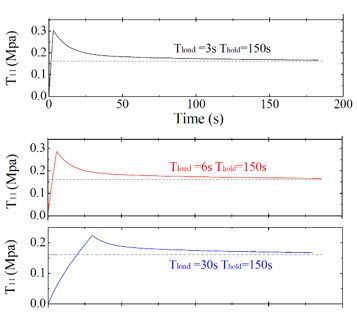
Figure 22. Reference result with 3s, 6s and 30s Tload
The uniaxial tension data at the two extrapolated environments is used as the input data.
Results
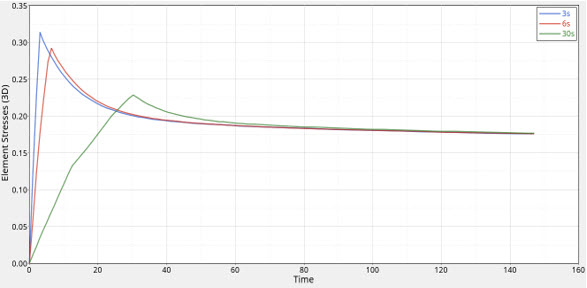
Figure 23. Elemental stresses with 3s, 6s, and 30s Tload