Rotor Dynamics
Rotor Dynamics is the analysis of structures containing rotating components.
The dynamic behavior of such structures is influenced by the type and angular velocity of rotating components and their locations within the model. Rotor dynamics is available in OptiStruct for modal frequency response, complex eigenvalue, static, linear direct transient and small displacement nonlinear direct transient analyses.
Motivation

Figure 1. Application of Rotor Dynamics Analysis
In Figure 1, the rotating components of the structure are the shafts on which gears are mounted. The design of the rotors and their angular frequencies can affect the dynamic response of the structure. Any design will most likely lead to asymmetrical mass distribution about the rotor axes. This unbalanced mass, even if it is not significant, can result in deflection of the rotor depending on various factors. The magnitude of these deflections will be augmented when the rotating speed of the shafts equals the natural frequency of the structure (Resonance), and can lead to catastrophic failure of the system.
Implementation
The Rotor Dynamics functionality is activated in OptiStruct with the use of the RGYRO Subcase Information Entry (RGYRO=ID). This RGYRO entry references the identification number of a RGYRO Bulk Data Entry. Related Bulk Data Entries, RSPINR, UNBALNC, ROTORG and RSPEED are defined in the model for Rotor Dynamics. Parameters PARAM,GYROAVG, PARAM,WR3, and PARAM,WR4 are also used.
Whirl
A rotor is a structure that rotates about its own axis at a specific angular velocity. If a lateral force is applied to the rotor, it will deform in the lateral direction. This deformation is dependent on various factors, such as, magnitude of the applied force, rotor material properties, stator stiffness, and damping within the system. Due to rotor rotation, the deformed rotor will also whirl about an axis.
Synchronous and Asynchronous Analysis

Figure 2. Types of Whirl and the Two Analysis Types that are Dependent on the Angular Frequency of a Rotor
Forward Whirl and Backward Whirl
The type of whirl depends on the spin direction of a rotor. If the rotor spin direction is the same as that of its whirl direction, then it is termed as forward whirl. If the rotor spin direction is opposite to the whirl direction, it is termed as backward whirl. In complex eigenvalue analysis, you can determine and differentiate between the modes of a structure undergoing backward whirl and forward whirl.
Supported Solution Sequences
OptiStruct supports the Rotor Dynamics functionality in the following solution sequences.
Frequency Response Analysis
The response of a structure with rotating components to a specified external excitation can be determined using the rotor dynamics functionality in frequency response analysis.
Asynchronous analysis (RGYRO=ASYNC)
If ASYNC is specified in the RGYRO Bulk Data Entry, the rotors within the structure have user-defined spin rates. The excitation frequency (FREQi entries) is independent of the reference rotor speed defined in the RGYRO Bulk Data Entry.
Synchronous analysis (RGYRO=SYNC)
If SYNC is specified in the RGYRO Bulk Data Entry, the reference rotor spin rate is equal to (or synchronous with) the excitation frequency. The reference rotor speed is not input via the RGYRO Bulk Data Entry and the FREQi entry values are used in this analysis.
Complex Eigenvalue Analysis
The eigenvalues and critical speeds of a structure with rotating components can be determined using the rotor dynamics functionality in complex eigenvalue analysis.
Asynchronous analysis (RGYRO=ASYNC)
If ASYNC is specified in the RGYRO Bulk Data Entry, the rotors within the structure have user-defined spin rates via the RSPEED entry and the Campbell Diagram can be plotted to find the critical speeds. Additionally, since the calculated eigenvalues are complex, you can determine unstable modes by studying the real parts of the calculated eigenvalues. If the real part of a complex eigenvalue is positive, then the corresponding system mode is unstable.
Synchronous analysis (RGYRO=SYNC)
Frequency Response Analysis (ASYNC)
The response of a system with rotating components to an external load in the frequency domain is calculated based on Equation 1.
Frequency Response Analysis (SYNC)
The response of a system with rotating components to a rotor imbalance which is considered as a force acting in the frequency domain is calculated based on Equation 2.
Frequency Response Analysis with WR3, WR4 and WRH (ASYNC)
Frequency Response Analysis with WR3, WR4 and WRH (SYNC)
Complex Eigenvalue Analysis with WR3, WR4 and WRH (ASYNC)
Complex Eigenvalue Analysis with WR3, WR4 and WRH (SYNC)
Static
Linear and Small Displacement Nonlinear Direct Transient Analyses
Where,
is the reference rotor spin rate
is the spin rate of rotor "" as a function of the reference rotor spin rate.
Where,
and are scaling factors calculated from the relative spin rates defined in the RSPINR Bulk Data Entry.
is the structural mass
is the viscous damping of the support
is the rotor viscous damping
is the rotor hybrid viscous damping
is the rotor mass
is the rotor stiffness
is the rotor material damping
is the rotor hybrid material damping
is the circulation, due to rotor viscous damping
is the circulation due to rotor hybrid viscous damping
is the circulation, due to rotor mass
is the circulation, due to rotor structural stiffness
is the circulation, due to rotor material damping
is the circulation, due to rotor hybrid material damping
is the stiffness of the support
is the material damping of the support
is the number of rotors in the model
is the displacement as a function of frequency
is the displacement as a function of reference rotor spin rate
is the external excitation as a function of frequency
is the unbalanced load as a function of reference rotor spin rate (via DAREA or UNBALNC entries)
is the structural damping value of the support defined using PARAM,G
is the structural damping value of the rotor defined using PARAM,G
is the angular velocity vector obtained from a pertinent RFORCE entry
WR3, WR4, and WRH are defined via the parameters PARAM, WR3, PARAM, WR4, and PARAM, WRH. They may also be rotor dependent and specified on RSPINR and RSPINT Bulk Data Entries. These parameters allow you to bypass frequency-dependent looping by specifying the equivalent “average” excitation frequencies when PARAM, GYROAVG, -1 is specified.
- Regular damping matrix
- Skew-symmetric rotation matrix defined as follows in the rotor coordinate system
- Gyroscopic matrix defined in a rotor coordinate system
as:
(12)
Model Guidelines
1D Rotor Model
The OptiStruct rotor dynamics feature currently supports only 1D rotors. Rotor shafts modeled with 1D elements like CBEAM, CBAR, or CBUSH only can be used. CONM1 or CONM2 entries should be used to define the mass and inertia of the rotors. Grid points are necessary for the definition of mass and inertia via CONM1 or CONM2. All grid points that belong to rotors should be listed in the ROTORG entries and only grids listed in the ROTORG entries are included in the calculation of gyroscopic terms. The Ixx fields on the CONM2 entry should contain meaningful values as only the inertia about the local X, Y, or Z axes plays a role in the gyroscopic forces (Supported Solution Sequences section). If CONM1 entries are used, the Mxy mass values should be specified such that the moments of inertia about the local X, Y, or Z axes are meaningful.
Detached Rotor Model
The rotor should be detached from the rest of the structure. Only rigid elements (RBEi) can be used to attach rotors to the ground or to flexible bearings. If any connection exists between the rotor and other parts of the structure using elements other than RBEi, then the program will error out.
Symmetric Rotor in a Fixed Reference Frame
Rotor dynamics analysis in OptiStruct is performed based on assumption that the rotor is symmetric. Therefore, the rotor model is required to be symmetric about the rotation axis. The implementation is based on equations of motion formulated in a fixed reference frame. Asymmetric rotors in a rotating reference frame is planned to be implemented in future versions of OptiStruct.
Rotor-axis Guidelines
- These grids are permitted to have a user-defined input coordinate system. As the rotor axis is dependent on the input coordinate system, this definition would change the direction of the rotor axis.
- These grids can also have a user-defined output coordinate system. The output coordinate system does not affect the direction of the rotor axis.
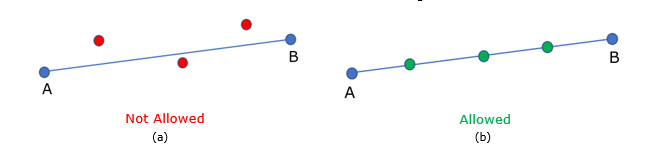
Figure 3. Grid Points Definition. (a) outside line AB; (b) on line AB
Multiple Rotors
During synchronous analysis, the calculations are performed with respect to the reference rotor. In synchronous frequency response analysis, the reference rotor is rotating at the frequency of the unbalanced load and in synchronous complex eigenvalue analysis, the reference rotor is rotating at the whirl frequency of the system. The interpretation of results in a multiple rotor system should always be done with respect to the reference rotor. Any deduction of results from the behavior of rotors other than the reference rotor will be inaccurate and can lead to incorrect results. If the behavior of a rotor other than the reference rotor is to be studied, a different analysis should be run with the rotor of interest as the reference rotor.
- Co-axial
- Rotors share the same axes of rotation
- Multi-axial
- Rotors have different axes of rotation
Campbell Diagram
The critical speeds of a rotating structure should be calculated and the design parameters can then be altered if necessary to restrict the operating speeds of the structure from attaining those resonant speeds.
- Synchronous Complex Eigenvalue AnalysisThe RGYRO=SYNC option in Complex Eigenvalue Analysis can be used to determine the exact critical speeds of the rotating structure. During a synchronous analysis, the rotor speed is equal to the whirl frequency of the structure, which by definition, are the critical speeds of the structure that should be avoided during its operation.
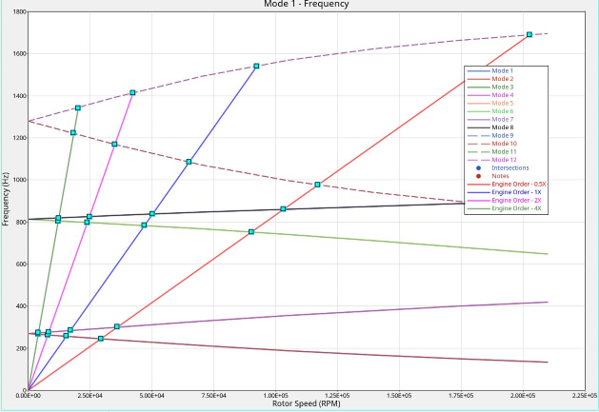
Figure 4. Campbell Diagram to Calculate the Critical Speeds - Asynchronous Complex Eigenvalue AnalysisThe RGYRO=ASYNC option and the RSPEED Bulk Data Entry in Complex Eigenvalue Analysis can be used to determine the whirl frequencies (backward whirl and forward whirl) of the structure. These Whirl frequencies can be calculated for a sequence of rotor spin rates. Forward Whirl and Backward Whirl frequencies can then be plotted against the range of rotor spin rates (Figure 4). The critical speeds can be calculated by superimposing the "Rotor Spin Rate = Whirl Frequencies" line on the plot. The points of intersection are the critical speeds.Note: The rotor speeds specified on the RSPEED entry should be input with sufficiently fine resolution to be able to capture the critical speeds. If the specified rotor speeds are too far apart, the critical speeds may be missed.
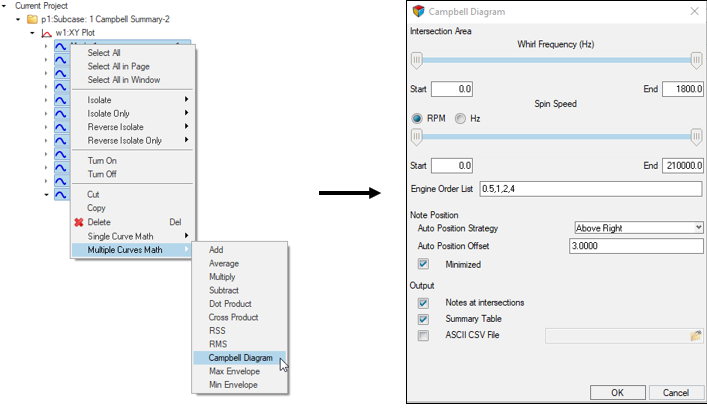
Campbell Diagram in HyperGraph 2D
The procedure to create the Campbell Diagram in HyperGraph 2D is:
Rotor Superelements
Rotors in frequency response and complex eigenvalue solutions can be replaced using superelements.
Output
Subcase: 1
Campbell Diagram Summary
Mode #: 1
-------------------------------------------------------------------------------
Step Rotor speed Eigenvalue Eigenvalue Frequency Damping Whirl
(RPM) (Re) (Im) (Hz)
-------------------------------------------------------------------------------
1 0.000E+00 -1.92148E-01 -3.81017E+02 6.064E+01 1.009E-03 LINEAR
2 2.000E+02 -1.92108E-01 -3.81011E+02 6.064E+01 1.008E-03 BACKWARD
3 4.000E+02 -1.91987E-01 3.80993E+02 6.064E+01 1.008E-03 BACKWARD
4 6.000E+02 -1.91788E-01 -3.80964E+02 6.063E+01 1.007E-03 BACKWARD
5 8.000E+02 -1.91513E-01 3.80924E+02 6.063E+01 1.006E-03 BACKWARD
6 1.000E+03 -1.91163E-01 3.80873E+02 6.062E+01 1.004E-03 BACKWARD
7 1.200E+03 -1.90742E-01 3.80810E+02 6.061E+01 1.002E-03 BACKWARD
Mode #: 2
-------------------------------------------------------------------------------
Step Rotor speed Eigenvalue Eigenvalue Frequency Damping Whirl
(RPM) (Re) (Im) (Hz)
-------------------------------------------------------------------------------
1 0.000E+00 -1.92148E-01 3.81017E+02 6.064E+01 1.009E-03 LINEAR
2 2.000E+02 -1.92108E-01 3.81011E+02 6.064E+01 1.008E-03 BACKWARD
3 4.000E+02 -1.91987E-01 -3.80993E+02 6.064E+01 1.008E-03 BACKWARD
4 6.000E+02 -1.91788E-01 3.80964E+02 6.063E+01 1.007E-03 BACKWARD
5 8.000E+02 -1.91513E-01 -3.80924E+02 6.063E+01 1.006E-03 BACKWARD
6 1.000E+03 -1.91163E-01 -3.80873E+02 6.062E+01 1.004E-03 BACKWARD
7 1.200E+03 -1.90742E-01 -3.80810E+02 6.061E+01 1.002E-03 BACKWARD- In rare cases, when the job is run in different machines, a given model might show flip in the sign of imaginary eigenvalues between a pair of modes. This is due to numerical differences while ordering the modes.
- As the roots are complex conjugates, if the sign changes for a particular step (that is, rotor speed) in a mode, then the same step will have opposite sign in a consecutive mode.