Basis Functions

Categories of Basis Functions

Entire-domain basis functions are defined over the entire surface of the scatterer - they are non-zero over the entire domain. The formulation of these functions is deemed rather trivial, provided the shape of the scatterer is regular. For most practical applications, the shape of the scatterer is irregular and the formulation of such basis functions is near impossible. This requires the usage of sub-domain basis functions.

Types of Sub-Domain Basis Functions

The Rao-Wilton-Glisson (RWG) element

The MoM in Feko is based on a triangular mesh. Triangular meshes can approximate surfaces much better than for example, rectangular patches. Feko makes use of linear roof-top basis functions introduced by Rao, Wilton and Glisson in 1982. ¹ These basis functions enforces current continuity over a common edge of a triangle pair.

Figure 1. A triangle pair showing the current flow across the common edge as modelled by the RWG basis function.

In Figure 1, only two triangles are shown sharing a common edge. Each triangle also has two other edges. If these edges are connected to triangles, then additional basis functions would be required. Therefore for a triangle connected on all three sides, a total of three basis functions would be defined. Within the triangle element the total current would then be the sum of these three basis functions.

In Figure 5, the Yagi-Uda was modelled with wire segments. Similar to triangle pairs, linear roof-top basis functions are used across vertices between wire segment pairs.

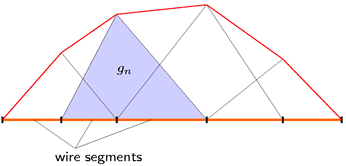
Figure 2. Linear roof-top basis functions for wires modelling current across the wire vertices.