Equations de Maxwell pour un système électrique
Introduction
Les équations de Maxwell sont les lois fondamentales de l'électromagnétisme.
Elles lient la densité de charges
électriques et la densité de courant électrique 
présents dans un système, aux champs qui en
résultent :
- champ
électrique
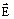et induction
électrique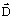 
-
induction magnétique
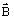et champ
magnétique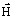 
Forme générale des équations
La forme générale des équations de Maxwell est la suivante :
Maxwell-Gauss : 
(1)
Maxwell-Faraday : 
(2)
Conservation du flux magnétique : 
(3)
Maxwell-Ampère 
(4)
Autres équations
A ces équations viennent s'ajouter les équations constitutives de la matière :
Caractéristique des milieux conducteurs : 
(5)
Caractéristique des milieux magnétiques: 
(6)
(7)- σ est la conductivité du milieu (en S)
- μ est la perméabilité du milieu (en H/m)
- ε est la permittivité du milieu (en F/m)
Séparation
A basse fréquence, les équations en
champs électriques 
et 
et les
équations en champs magnétiques 
et 
peuvent être découplées.
Les équations de Maxwell peuvent alors s'écrire différemment pour les systèmes magnétiques et les systèmes électriques :
- une écriture pour les systèmes magnétiques
- une écriture pour les systèmes électriques
Cette séparation dépend : des matériaux, des fréquences de travail, de la taille du domaine d'étude. Elle est habituellement considérée comme valide pour des fréquences f < 1 à 10 GHz.
Forme des équations pour un système électrique
Pour un système électrique, on suppose que le champ magnétique ne modifie pas la
distribution de courant 
dans les conducteurs. Cette hypothèse reste vraie tant que la fréquence ne dépasse
pas une certaine limite. Cela se traduit par la nullité du terme 
dans l'équation 2.
Les équations peuvent alors s'écrire de la façon suivante :
Maxwell-Gauss : 
(1)
Maxwell-Faraday : 
(2)
Maxwell-Ampère : 
(4)
Caractéristique des milieux conducteurs : 
(5)
Caractéristique des milieux diélectriques : 
(7)