Magnétique Transitoire : équations résolues (modèle vecteur 2D)
Introduction
Le modèle vecteur est le modèle général proposé pour une application 2D.
Equation résolue en modèle vecteur (2D)
L'équation de Maxwell-Faraday : ![]() implique l'existence d'un potentiel scalaire électrique V tel
que :
implique l'existence d'un potentiel scalaire électrique V tel
que : ![]()
L'équation résolue par la méthode des éléments finis dans une application magnétique transitoire par la méthode des éléments finis s'écrit :
![]()
où:
- [νr] est le tenseur de réluctivité magnétique du milieu
- ν0 est la réluctivité du vide ; ν0 = 1/μ0 = 1/(4 π 10-7) (en m/H)
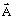 est le potentiel
vecteur magnétique (en Wb/m)
est le potentiel
vecteur magnétique (en Wb/m)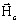 est le champ
coercitif (aimants) (en A/m)
est le champ
coercitif (aimants) (en A/m)- σ est le tenseur de conductivité du milieu (en S)
- V est le potentiel scalaire électrique (en V)
Variable d'état modèle vecteur (2D)
Les variables d'état sont :
- le
potentiel vecteur magnétique
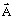
- le potentiel scalaire électrique V
La variable d'état, en fonction du type de problème (plan ou axisymétrique), est donnée dans le tableau ci-dessous.
| Type de problème |
Variable d'état |
Notation (dans Flux 3D) |
|---|---|---|
| plan | An | AN1* |
| axisymétrique | r.An | RAN1* |