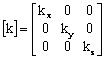Milieu isotrope / anisotrope
Introduction
Le milieu étudié peut être isotrope ou anisotrope . Autrement dit, la conductivité thermique peut être :
-
indépendante de la direction du gradient de température appliqué (milieu isotrope)
-
dépendante de la direction du gradient de température appliqué (milieu anisotrope)
Ces deux cas sont présentés dans les blocs ci-après.
Milieu isotrope
Les milieux isotropes sont caractérisés par une conductivité thermique indépendante de la direction du gradient de température appliqué.
Les vecteurs 
et 
sont
toujours colinéaires.
La relation entre 
et 
est une
relation scalaire
qui s'écrit : 
Milieu anisotrope
Les milieux anisotropes sont caractérisés par une conductivité thermique dépendante de la direction du gradient de température appliqué.
Les vecteurs 
et 
ne sont
pas colinéaires.
La relation entre 
et 
est une
relation vectorielle
qui s'écrit : 
avec [k] tenseur de conductivité :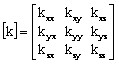 
… dans Flux
Le modèle proposé dans Flux est un modèle simplifié.
La relation vectorielle entre 
et 
qui s'écrit : 
peut alors se mettre sous la forme de 3 courbes :
, 
, 
Le tenseur de conductivité s'écrit
alors : 