Fit a Curve by Estimating UTS
An empirical formula can be used to estimate SN/EN data from ultimate tensile strength (UTS) and Young's modulus (E).
- From the Assign Material dialog, click the My Material tab and select your created material.
- Select Estimate from UTS as the input method.
-
Click
 to view the model
description.
to view the model
description.
- Enter a value for UTS and Elastic modulus.
- Click Estimate.
SN Properties
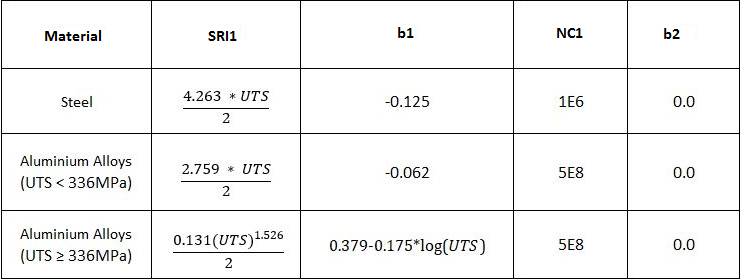
Figure 1. SN Method Description
- Fatigue strength coefficient. It is the stress amplitude intercept of the SN curve at 1 cycle on a log-log scale.
- The first fatigue strength exponent. The slope of the first segment of the SN curve in log-log scale.
- In one-segment SN curves, this is the cycle limit of endurance (See Nc1 in Figure 2). In two-segment SN curves, this is the transition point (see Nc1 in Figure 4).
- The second fatigue strength exponent.
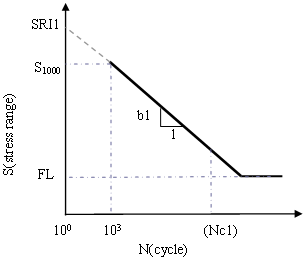
Figure 2. One-segment SN curve in log-log scale (b2=0) (Nc1 is not defined or less conservative than FL)
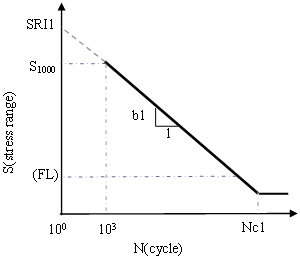
Figure 3. One-segment SN curve in log-log scale (b2=0) (FL is not defined or less conservative than Nc1)
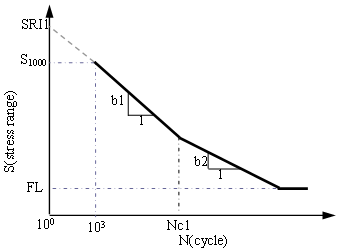
Figure 4. Two-segment SN curve in log-log scale
EN Properties
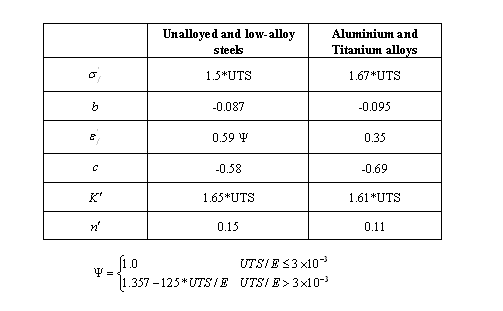
Figure 5. EN Method Description
- Fatigue strength coefficient.
- Fatigue strength exponent.
- Fatigue ductility exponent.
- Fatigue ductility coefficient.
- Cyclic strain-hardening exponent.
- Cyclic strength coefficient.
- Reversal limit of endurance. One cycle contains two reversals.
- Standard Error of Log(N) from elastic strain.
- Standard Error of Log(N) from plastic strain.
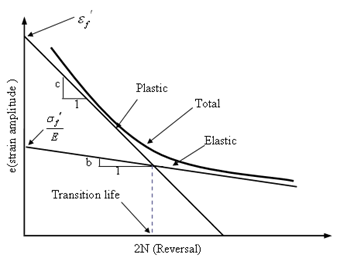
Figure 6. EN curve in log-log scale