OS-E: 2030 Cantilever Beam Modeled with Solid Elements
The purpose of this example is to minimize the volume of a prismatic cantilever beam.
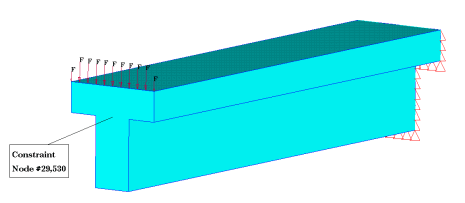
Figure 1. Cantilever Beam; Loads and Boundary Conditions
Model Files
Refer to Access the Model Files to download the required model file(s).
The model file used in this example includes:
beam_shape.fem
Model Description
The maximum displacement at the beam tip is limited, and the 1st and 2nd eigen frequencies have a lower bound. Two subcases are defined; subcase 1 is the static load case, subcase 2 is the eigenmode analysis.
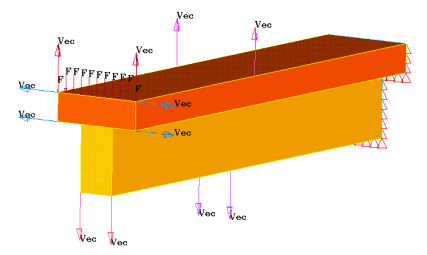
Figure 2. Cantilever Beam; Design Elements and Design Variables
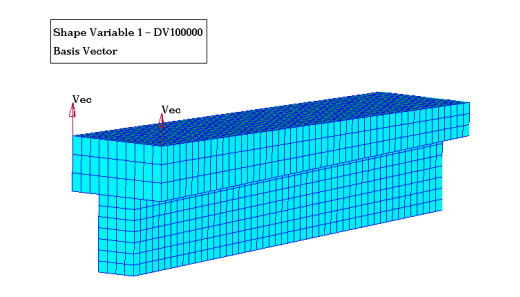
Figure 3. Cantilever Beam; Perturbed Shape Number 1
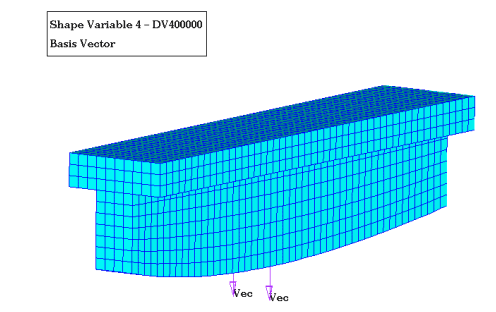
Figure 4. Cantilever Beam; Perturbed Shape Number 4
The perturbation vectors need to be provided in the format of the DVGRID cards using AutoDV (part of HyperMesh). These cards can be generated automatically. The output of AutoDV also includes the design variable definition DESVAR. The output file Beam_shape.dat can be incorporated into the Bulk Data section of the OptiStruct input deck via an include statement.
Results
The definition of the optimization problem is included in the case control section of the input deck. Figure 5 shows the section of the OptiStruct input file that includes the definition of the optimization problem and the inclusion of the AutoDV output.
$-----------------------------------------------------------------
$
$ Case Control Cards
$
$-----------------------------------------------------------------
$
DESOBJ(MIN) = 1
$
$HMNAME LOADSTEPS 1Static
$
SUBCASE 1
LOAD = 2
SPC = 3
DESSUB = 101
$
$HMNAME LOADSTEPS 2Eigenvalues
$
SUBCASE 2
SPC = 3
METHOD = 4
DESSUB = 201
$
BEGIN BULK
INCLUDE Beam_shape.dat
$
$ LOAD cards
$
EIGRL, 4, , , 10
$
DRESP1, 1, vol, VOLUME
DRESP1, 2, disp, DISP,,,2,,29530
DCONSTR, 101, 2, -0.01
DRESP1, 3, f1, FREQ,,,1
DRESP1, 4, f2, FREQ,,,2
DCONSTR, 202, 3, 2600.0
DCONSTR, 203, 4, 3000.0
DCONADD, 201, 202, 203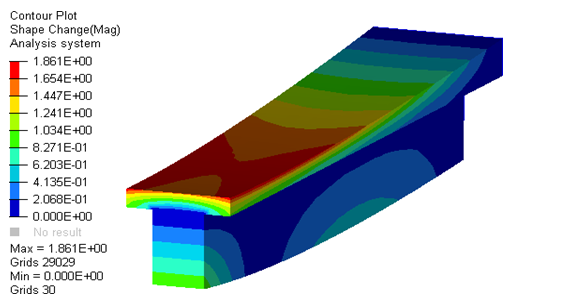
Figure 5. Cantilever Beam; Final Shape