OS-V: 0270 Torsional Creep of Circular Shaft

This benchmark illustrates the structural response of a power law creeping material in a geometrical configuration subjected to pure torsion. OptiStruct examines strain at the edge of the shaft.

The model examines the torsional creep in circular shaft with 2 variations:
  • Relaxation at constant twist
  • Forward creep at steady twist rate

Relaxation at Constant Twist

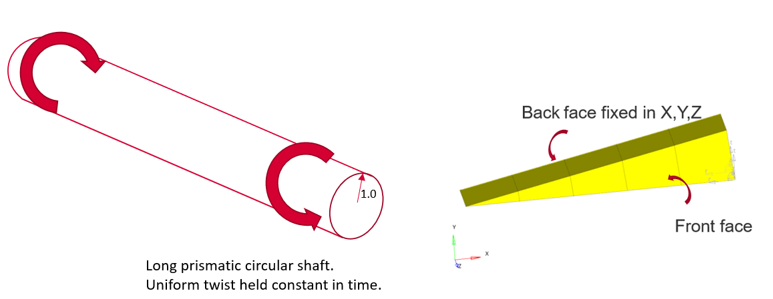
Twist is applied to the shaft and remains constant from 0 to 100s. Total strain and creep strains then analyzed.


Figure 1. Model and Loading Description

Benchmark Model

Four 20-noded brick elements, plus one 16-noded wedge are used. All nodes on lower face are fixed in X, Y, Z.
  • X, Y displacements given at all nodes of front face using cylindrical system: 0.002 mm
  • Rotation is given at mid-side nodes: 0.001 radians

Uniform twist of 0.01 radians/unit length is held constant in time from 0 to 100s.

Twist is instantaneously applied to the shaft and then maintained constant. The initial response is elastic and subsequently the structure response with a progressive accumulation of creep strain. Stress reduces (relaxes) slowly till 100s due to creep.
Material Properties
Value
Young's modulus
10 GPa
Poisson's ratio
0.3
Creep law equation
ε ˙ eq =1000  σ 5 eq MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGafqyTduMbai aadaWgaaWcbaGaamyzaiaadghaaeqaaOGaeyypa0JaaGymaiaaicda caaIWaGaaGimaiaabccacqaHdpWCdaahaaWcbeqaaiaaiwdaaaGcda WgaaWcbaGaamyzaiaadghaaeqaaaaa@4313@
Where,
ε ˙ eq MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGafqyTduMbai aadaWgaaWcbaGaamyzaiaadghaaeqaaaaa@39B2@
Equivalent creep strain rate
σ eq MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aaS baaSqaaiaadwgacaWGXbaabeaaaaa@39C5@
Equivalent stress (Mises)

Nonlinear Static Analysis Results

An implicit visco-elastic solution method was used. Displacement, total strain and creep strain results are analyzed at the edge of the shaft at 100s.
OptiStruct NAFEMS Normalized Target Value
Total Strain (*10-3) 5.46 5.77 0.95
Creep Strain (*10-3) 4.85 4.77 1.01
Comparison of strain plots.


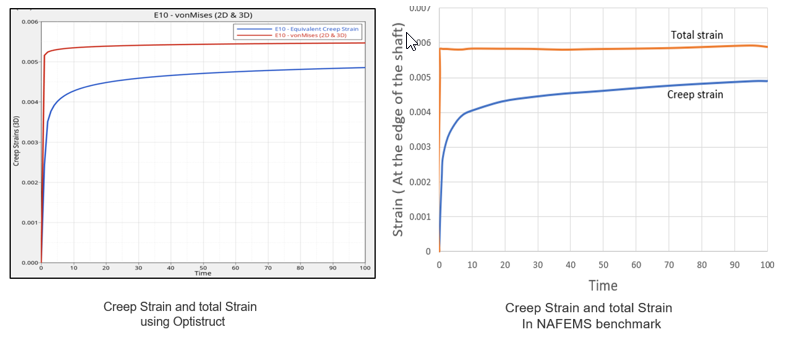
Figure 2. Comparison of Total Strain and Creep Strain at the Edge of the Shaft

Model Files

Refer to Access the Model Files to download the required model file(s).

The model file used in this example includes:

Torsional_Creep_Relaxation_at_constant_twist.fem

Forward Creep at Steady Twist Rate

A steadily increasing twist is applied at constant rate to the shaft.

The stresses increase from zero to steady value. The loads, which cause this steady-state behavior are referred as “primary” loads.

This model is the same as used in Relaxation at Constant Twist; except the boundary conditions.


Figure 3. Model and Loading Description

Benchmark Model

Four 20-noded brick elements, plus one 16-noded wedge are used. All nodes on lower face are fixed in X, Y, Z.
  • X, Y displacements given at all nodes of front face using cylindrical system: 0.004 mm/unit time
  • Rotation is given at mid-side nodes: 0.002 radians/unit time
Uniform twist of 0.02 radians/unit time is steadily increating with time from 0 to 1.5 applied using table curve.
Material Properties
Value
Young's modulus
10 GPa
Poisson's ratio
0.3
Creep law equation
ε ˙ e q = 1000   σ 5 e q MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGafqyTduMbai aadaWgaaWcbaGaamyzaiaadghaaeqaaOGaeyypa0JaaGymaiaaicda caaIWaGaaGimaiaabccacqaHdpWCdaahaaWcbeqaaiaaiwdaaaGcda WgaaWcbaGaamyzaiaadghaaeqaaaaa@4313@
Where,
ε ˙ e q MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGafqyTduMbai aadaWgaaWcbaGaamyzaiaadghaaeqaaaaa@39B2@
Equivalent creep strain rate
σ e q MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aaS baaSqaaiaadwgacaWGXbaabeaaaaa@39C5@
Equivalent stress (Mises)

Nonlinear Static Analysis Results

An implicit visco-elastic solution method was used. Displacement, total strain and creep strain results are analyzed at the edge of the shaft at 1.5s.
OptiStruct NAFEMS Normalized Target Value
Total Strain (*10-2) 1.62 1.7321 0.94
Creep Strain (*10-2) 1.27 1.1693 1.094
Comparison of strain plots.


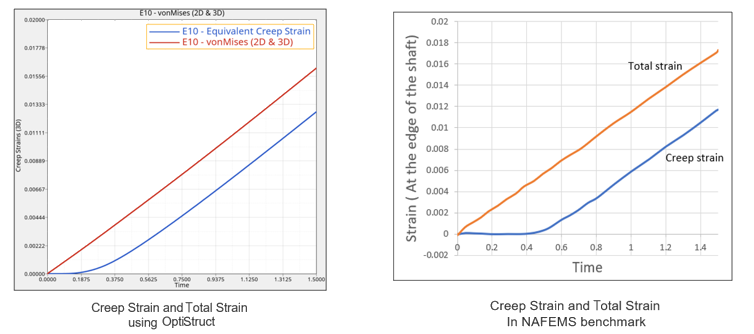
Figure 4. Comparison of Total Strain and Creep Strain at the Edge of the Shaft

Model Files

Refer to Access the Model Files to download the required model file(s).

The model file used in this example includes:

Torsional_forward_creep_at_steady_twist_rate.fem

Reference

NAFEMS R0026 - Selected Benchmarks for Material Non-Linearity- Volume 1