OS-E: 4005 Rotating Shell
In some models, the rate of change for the response value with respect to time is very high, and the response is dominant in the design process.
Model Files
Refer to Access the Model Files to download the required model file(s).
The model file used in this example includes:
rotating_shell_design.fem
Model Description
Figure 1. Rotating Shell

Figure 2. Profile of the Driving Motion
Results
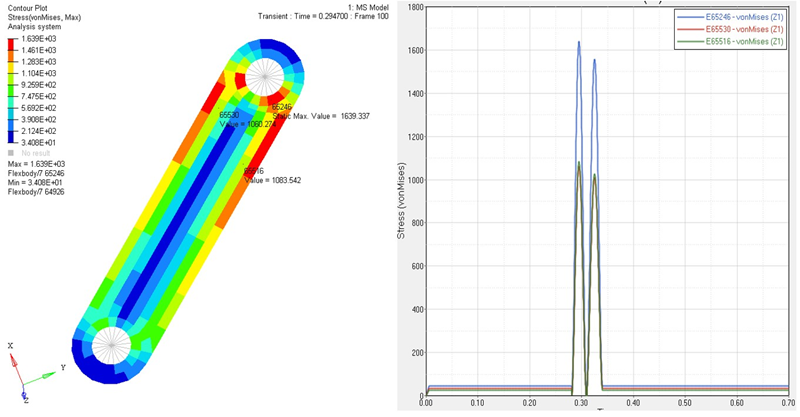
Figure 3. Analysis Result of the Initial Design
- Run an analysis model with reasonable number of steps in
MBSIM card.
ANALYSIS $ DESOBJ(MIN)=1 $ SUBCASE 1 MBSIM = 10 MOTION = 11 DESSUB = 11 SPC = 10 : : MBSIM 10 TRANS END 0.7 NSTEPS 100Now you can find out the behavior of the structure as in the analysis result image.
- According to the results post-processed by HyperView, the maximum stresses are
developed at around 0.3 seconds. Increase the number of time
steps around 0.3 seconds. That is, divide the time period of
0.28 seconds – 0.34 seconds into 200 steps. Increasing the
number of time steps in this period provides the optimizer with
more information.
The element that has the maximum stress and the corresponding time can be changed as the design changes. Thus, Step 2 does not always work. If the time when maximum stress is developed and corresponding element are expected to change dramatically as the design changes, it is best to consider the changed peak time and corresponding element as much as possible.
- Replace the previous single MBSIM card with
multiple MBSIM cards as the following.
MBSIM 1 TRANS END 0.28 NSTEPS 50 + VSTIFF MBSIM 2 TRANS END 0.34 NSTEPS 200 + VSTIFF MBSIM 3 TRANS END 0.70 NSTEPS 50 + VSTIFF MBSIM 4 TRANS END 1.0 NSTEPS 100 + VSTIFF MBSEQ 10 1 2 3 - Run the optimization problem by removing
ANALYSIS command.
$ANALYSIS DESOBJ(MIN)=1 $ SUBCASE 1 MBSIM = 10 MOTION = 11 DESSUB = 11 SPC = 10 : : MBSIM 1 TRANS END 0.28 NSTEPS 50 + VSTIFF MBSIM 2 TRANS END 0.34 NSTEPS 200 + VSTIFF MBSIM 3 TRANS END 0.70 NSTEPS 50 + VSTIFF MBSEQ 10 1 2 3
Using the above steps, the design process convergence can be enhanced.