RD-V: 0300 Pressure Loading
A block impacts a plate and the system momentum is compared to theory.
Figure 1.
The pressure loading of a plate was evaluated by comparing the plate momentum caused by a pressure loading to the theoretical momentum.
Options and Keywords Used
/PLOAD
Input Files
Refer to Access the Model Files to download the required model file(s).
The model files used in this problem are available in:
/radioss/verification/loads
Model Description
The plate is 254 mm square and 25.4 mm thick and is meshed with two elements through the thickness. The plate is modeled using solid elements and a linear elastic material. The plate is constrained to allow only motion in the z-direction.
The pressure curve is applied to the elements in the z=0 plane in the positive z direction. The pressure linearly increases to 2.7579 MPa in 50 microseconds. Next, the pressure exponentially decayed using a time constant of 0.0218 sec until 0.010 sec. Lastly, the load linearly decreases to zero pressure at 0.010001 sec until the simulation end time of 0.02 seconds. The pressure function uses a time increment of 1e-6 sec to match the time increment used in the estimation of the integral in analytical solution. 1
Using the /DTIX Engine command, the simulation was forced to have a timestep of 1e-6 to match the time analytical solutions time increment.
The following system is used: mm, s, Mg.
Results
Figure 2. Plate Z Momentum
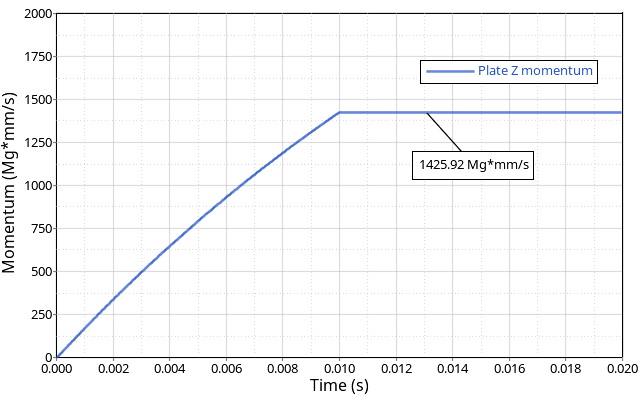
Conclusion
The numerical error is very small and the momentum from the finite element simulation closely matches the analytical solution.