Stresses in Solids
Principal Stresses
The diagonal components are called the principal stresses and allow a 3D representation of the state of stress at a point.
Stress Invariants
The values of these functions remain invariant under transformation by a proper orthogonal matrix. If,
then,
Invariant Space
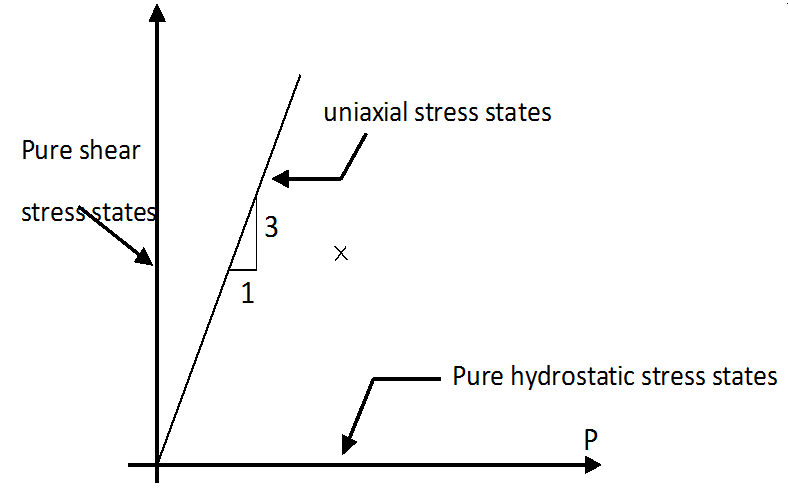
Figure 1.
The horizontal axis corresponds to the hydrostatic loading, the vertical axes to pure shear. The line with tangent 1/3 is uniaxial compression. The line with tangent -1/3 is uniaxial tension.
Deviatoric Stresses
The pressure or first invariant is related to the change in volume of the solid. The deviation from a hydrostatic state of stress is linked to the change in shape. The stress deviator is defined as:
A surface of constant von Mises stress in deviatoric space or principal deviatoric space is a sphere (in stress space it is a cylinder).