Solid-Shell Elements
Figure 1. Solid-Shell Elements Application
- Shear and membrane locking with the hybrid strain formulation 1 2, the hybrid stress 3, and the Assumed and Enhanced Natural Strain formulations. 4 5 6 7
- Trapezoidal locking caused by deviation of mid-plane from rectangular shape 8.
- Thickness locking due to Poisson's ratio coupling of the in-plane and transverse normal stresses. 1 2 4 6
Solid shell elements in Radioss are the solid elements with a treatment of the normal stresses in the thickness direction. This treatment consists of ensuring constant normal stresses in the thickness by a penalty method. Advantage of this approach with respect to the plane-stress treatment is that it can simulate the normal deformability and exhibits no discernible locking problems. The disadvantage is its possible small time step since it is computed as solid element and the characteristic length is determined often using the thickness.
- HA8: 8-node linear solid and solid-shell with or without reduced integration scheme,
- HSEPH: 8-node linear thick shell with reduced integration scheme and physical stabilization of hourglass modes,
- PA6: Linear pentahedral element for thick shells,
- SHELL16: 16-node quadratic thick shell.
The thick shell elements HA8 and HSEPH are respectively the solid elements HA8 and HEPH in which the hypothesis of constant normal stress through the thickness is applied by penalty method. The theoretical features of these elements are explained in Solid Hexahedron Elements. The thick shell element SHELL16 is described hereby.
Thick Shell Elements SHELL16
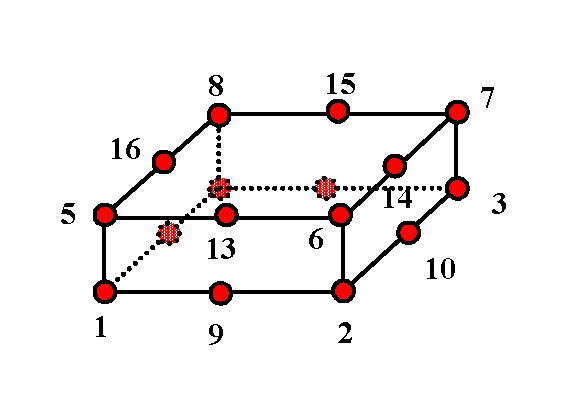
Figure 2. Thick Shell Element SHELL16
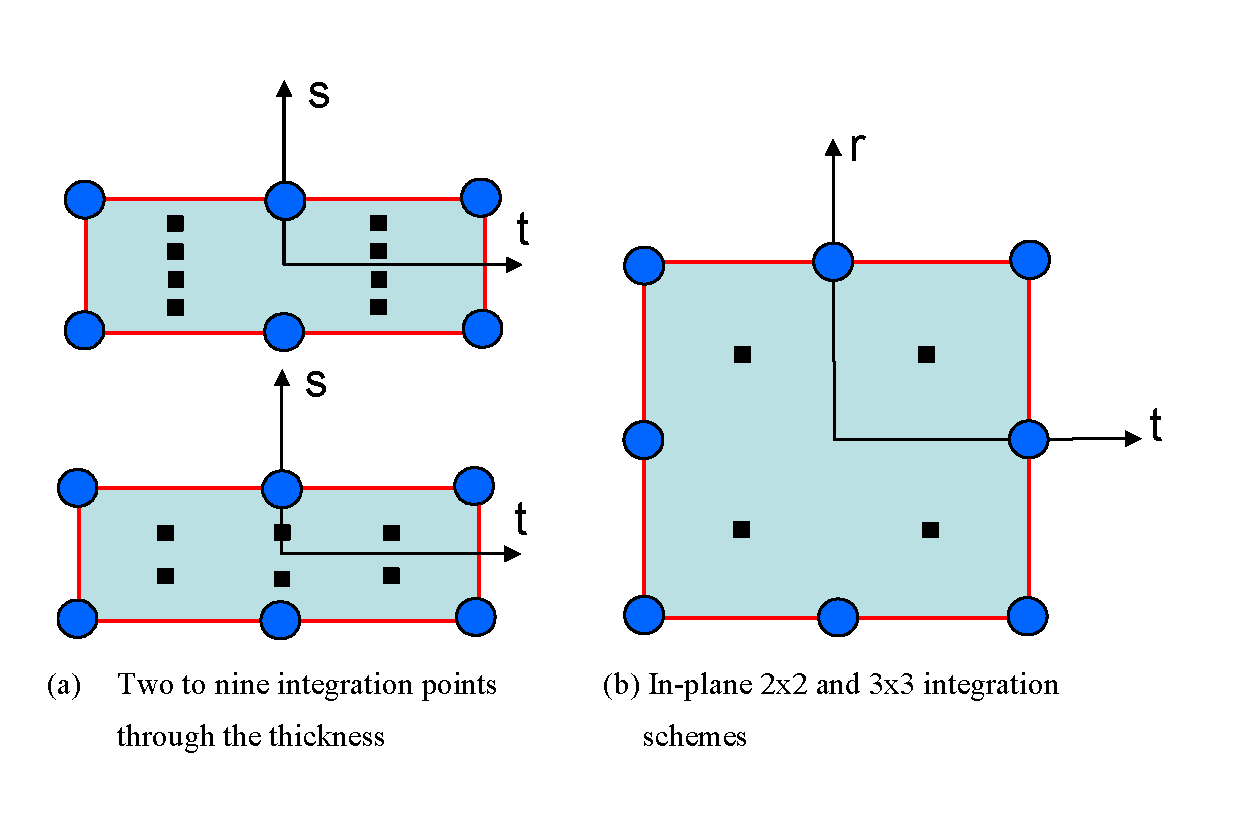
Figure 3. Integration Points for SHELL16
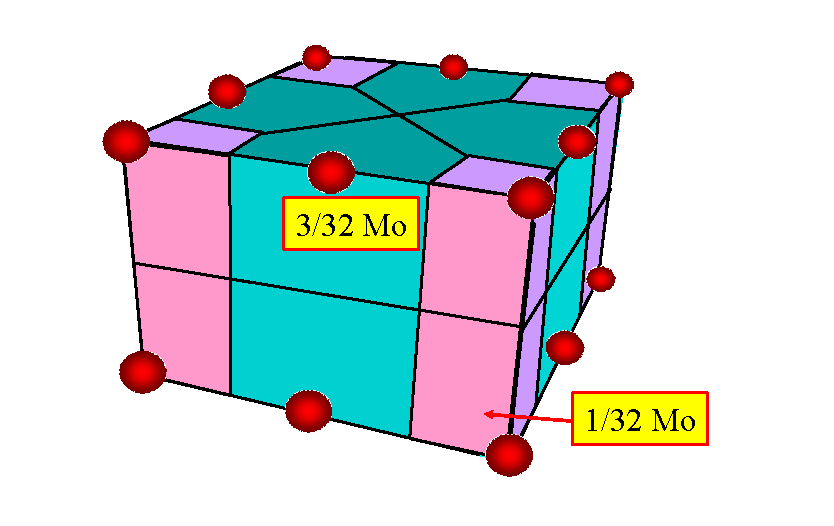
Figure 4. Mass Distribution for SHELL16 Element