Mass Injection
The amount of mass injected into the airbag needs to be defined with respect to time. This is required as a function.
The specific heat, , along with a function defining the change in temperature with time is required.
- Possibly from the airbag manufacturer
- From a tank experiment
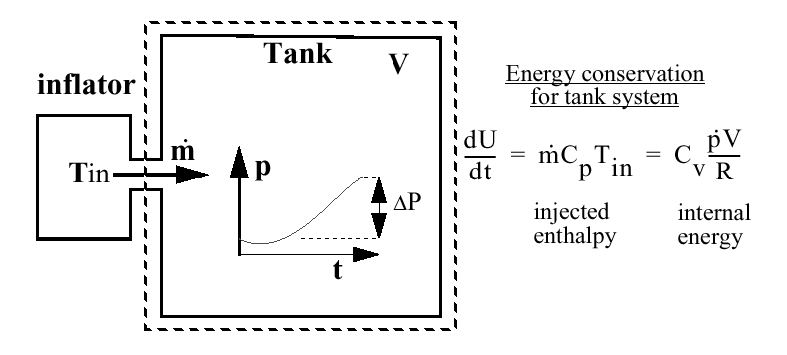
Figure 1. Tank Experiment
Where, is the molecular weight of the injected gas. is the perfect gas constant: ; .
- Total pressure variation during the experiment
- Total injected mass, which can be derived from the mass of propellant in the pyrotechnic inflator and the chemical reaction; 40% is a typical value for the ratio of the produced mass of gas to the solid propellant mass.