Initial conditions and boundary conditions

Introduction

The previous equations describe heat transfer by thermal conduction within the solid bodies of the temperature computation domain; they are characterized by the material properties k and ρCp and the volume density of the power of the heat sources q.

Other conditions of uniqueness of the solution of the heat transfer equation are the initial conditions and the boundary conditions at the surface of the solid body.

Initial conditions

The initial conditions describing the temperature field at the start (t = 0) of a transient thermal study can be of different types, for example:

  • Uniform temperature field in all the computation domain;
  • Non uniform temperature field; i. e. different values of the temperature at different points of the study domain (with initialization by FE solution)
Note: * cf. Transient thermal: initial conditions

Boundary conditions

The boundary conditions can be of different types:

  • Imposed T0 temperature on the boundary.

    This temperature can be time dependent and it can even be different at different points along the boundary. The simplest case is T = T0, constant over the entire boundary.

  • Heat flux density 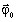imposed on the boundary.

    A heat flux density 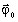is imposed on the boundary. This flux represents a heat source, reflecting the entering or exiting heat at the level of the computation domain boundary.

    The specific case φ0 = 0 means that the computation domain is thermally insulated (adiabatic boundary). There are no thermal exchanges between the solid body and its external environment on this boundary type.

  • The thermal exchange with the surrounding environment can be:
    • thermal exchange by convection: 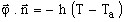,where:
      • h is the convection heat exchange coefficient in W/m2 /K,
      • T a is the ambient temperature in K;
    • thermal exchange by radiation to infinite: 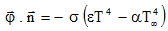, where:
      • ε is the radiation heat exchange coefficient (or emissivity)
      • σ = 5,675×10-8 W/m2/K4, the Stephan-Boltzmann constant;
      • α is the absorption coefficient
      • T ∝ is the virtual body's temperature which participates in the exchange