Periodicity: definition (structure)
Definition
The Periodicity entity is defined by:
- a name
- a type of periodicity
- position of periodicity planes
Name
The name to identify the periodicity is allocated automatically by Flux during the creation of this one.
The user cannot modify this name.
Types of periodicity: 2D domain
The periodicity types and the characteristics useful for their description are gathered in the table below.
| Translation | Included length | Offset position |
|---|---|---|
| along X | along the X axis | along the X axis |
| along Y | along the Y axis | along the Y axis |
| Rotation with angle | Included angle of the domain | Offset angle |
|---|---|---|
| about Z axis | about Z axis | with respect to the ZOX plane |
| Rotation with number of repetitions | Number of repetitions | Offset angle |
|---|---|---|
| about Z-axis | along Z | with respect to the ZOX plane |
Types of periodicity: 3D domain
The periodicity types and the characteristics useful for their description are gathered in the table below.
| Translation | Included length | Offset position |
|---|---|---|
| along X | along the X axis | along the X axis |
| along Y | along the Y axis | along the Y axis |
| along Z | along the Z axis | along the Z axis |
| Rotation with angle | Included angle of the domain | Offset angle |
|---|---|---|
| about X-axis | about X-axis | with respect to the XOY plane |
| about Y-axis | about Y-axis | with respect to the YOZ plane |
| about Z-axis | about Z-axis | with respect to the ZOX plane |
| Rotation with number of repetitions | Number of repetitions | Offset angle |
|---|---|---|
| about X-axis | along X | with respect to the XOY plane |
| about Y-axis | along Y | with respect to the YOZ plane |
| about Z-axis | along Z | with respect to the ZOX plane |
Composed periodicity (in 3D only)
The composed periodicity is a particular periodicity defined by the composition:
- of a rotation about an axis X (Y, Z respectively)
- of a symmetry with respect to the plane YOZ (ZOX, XOY respectively)
It is defined in the following manner:
- the first plane (P1) is defined by its angular position with respect to the main plane XOZ (XOY, ZOY respectively): offset angle (θ1)
-
the second plane (P2) is defined by a rotation of plane P1 about Z-axis
(X-axis, Y-axis respectively): rotation angle (θ2 - θ1)
The rotation angle about the axis (θ2 - θ1) is
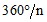where n is the number
of repetitive patterns (repetitions). - the third plane (P3) is defined by a symmetry of the plane P2 with respect to the symmetry plane: offset position of the symmetry plane on the Z rotation axis (X-axis, Y-axis respectively)
Important
It is not possible to change the type of the periodicity by editing its dialog box.
To change the periodicity type:
- Delete the periodicity
- Create a new periodicity
Length and angle units
Length and angle units are those associated with the domain.
These units can be edited and modified in the dialog box of the Domain Type.