Transformation: about
Principle of use
The transformations are geometric functions that permit the creation of new objects, starting from objects already created.
Various functions
The various available functions are:
- translation
- rotation
- affinity included symmetry
- composed transformation
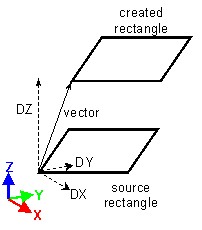
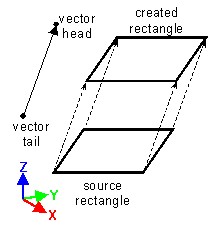
Translation
| Translation vector | Translation defined by two points and a ratio |
|---|---|
|
|
|
|
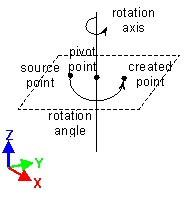
Rotation
A rotation is defined by a rotation axis and an angle.
| Rotation defined by three angles and a pivot point |
|---|
|
|
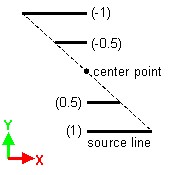
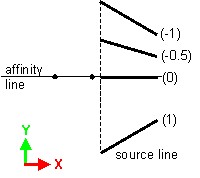
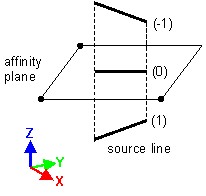
Affinity
Affinity is defined with respect to a point, to a straight line or to a plane.
The result of this transformation application depends on the affinity ratio (see the table below).
| Ratio | Result |
|---|---|
| k = -1 | symmetry |
| k = 1 | identity |
| k = 0 | projection |
| k > 1 | increasing (increasing affinity) |
| 0 < k < 1 | reducing (reducing affinity) |
| k < -1 | increasing (increasing negative affinity) |
| -1 < k < 0 | reducing (reducing negative affinity) |
| Affine transformation with respect to a point | Affine transformation with respect to a line | Affine transformation with respect to a plane |
|---|---|---|
|
|
 |
Symmetry
A symmetry is a particular case of affine transformation when k = -1 (see above); it is defined with respect to a point, a line or a plane.
Composed transformation
It is possible to create composed transformation combining the two already created transformations.
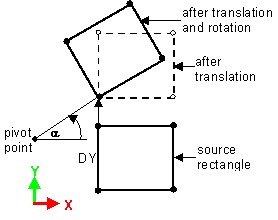
Transformation combining two transformations:
- a translation following Y-axis (defined by DX=0, and DY)
- a rotation about Z-axis (defined by the pivot point and an angle α)
Parameter setting
The characteristics of transformation are parametrized expressions. The vector components, the coordinates of pivot point, the rotation angles and the ratios of affinity can be defined using algebraic expression.
The algebraic expression can contain:
- constants
- geometric parameters (created beforehand)
- basic mathematical functions using operators: +, -, *, /, ( )
- usual mathematical functions admitted by FORTRAN
The mathematical functions are described in section Functions.